
How fast (in rpm) must a centrifuge rotate if a particle 7.00 cm from the axis of rotation is to experience an acceleration of 125,000 g’s?
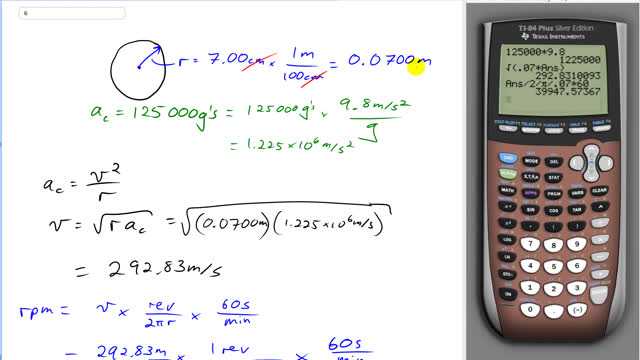
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. We'll convert this 7 centimeter radius into meters, by multiplying by 1 meter for every 100 centimeters; centimeters cancel giving us 0.0700 meters. The acceleration, 125000 g's; we'll convert that into meters per seconds squared by multiplying by 9.8 meters per seconds squared for every g, and the g's cancel giving us 1.225 times 10 to the 6 meters per second squared; always have to convert our units into mks units— meters, kilograms or seconds— when working with our formulas. So centripetal acceleration is v squared over r and we'll solve for v by multiplying both sides by r and then taking the square root of both sides to get v is the square root of radius divided by, or radius times centripetal acceleration. So, that's square root of 0.07 times 1.225 times 10 to the 6 meters per second; I used the second function enter to get, or second function negative sign to get the answer from the previous line. So that's what's there. That's 1225000 meters per second there. So, we get 292.83 meters per second, which is not the answer because they want us to tell the answer in rpm, revolutions per minute. So, we'll multiply this speed by how many revolutions you get for every, you know, 2πr meters. Every time you travel one circumference, that's what 2πr is, the circumference of the circle, you get 1 single revolution. So you get 1 revolution for every 2πr meters. And then we'll get rid of the seconds at the bottom here and turn it into minutes by multiplying by 60 seconds per minute. So, we have 292.83 meters per second; the meters are canceling, top and bottom, and the seconds are canceling, giving us revolutions per minute, rpm, and 292.83 divided by 2 divided by π divided by 0.07 meter— radius—times by 60 and you get 3.99 times 10 to the 4 revolutions per minute, rpm.