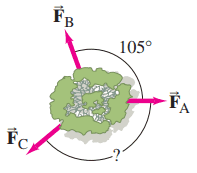
Three forces are applied to a tree sapling, as shown in Fig. 9–46, to stabilize it. If $\vec{F}_A = 385 \textrm{ N}$ and $\vec{F}_B = 475 \textrm{ N}$, find $\vec{F}_C$ in magnitude and direction.

VIDEO TRANSCRIPT

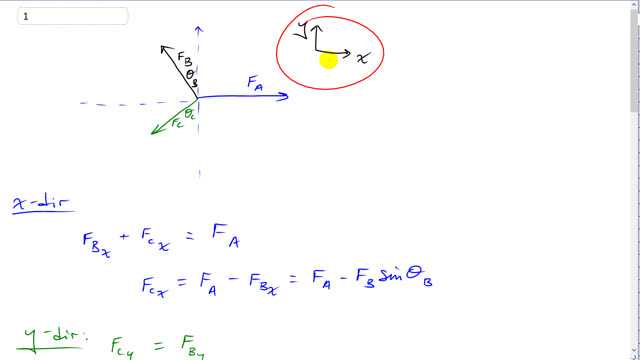
This is Giancoli Answers with Mr. Dychko. Since this tree sapling is in equilibrium it means all the forces balance out. So I have chosen a coordinate system so that one axis is along one of the forces we'll choose x-axis to be along force A and that will reduce our work a little bit because we don't have to worry about any trigonometry when we are dealing with force A— it's entirely in the x-direction. Now the force's balancing out means they balance out separately in the x-axis and along the y-axis so we'll have two different equations and so we can consider this x-component for force B up here pointing straight to the left that's F B x and that added to the x-component of force C, this is F C x those two have to equal the total x-forces going to the right which is just F A. So that's where this equation comes from and then we can solve for the x-component of force C by subtracting F B x from both sides. And then we'll replace F B x with F BsinΘ B where I have taken Θ B to be this angle between the vertical y-axis and the force and so we are gonna calculate that as being 105 minus 90, just 15 degrees. And F B x is the opposite leg of this triangle so we take sin of Θ B to get the opposite leg multiplied by the hypotenuse F B. Okay. And then the same idea for the y-direction and in the y-direction, there are only two forces to consider since force A is entirely in the x-direction. So the component of force B that's vertical, upwards, this is F B y has to equal the component of force C which is downwards, that's F C y. So F C y is F B times cos Θ B— cos is what we use to find the adjacent leg of the triangle— and here I mention again that Θ B is 105 degrees from force A minus the 90 degrees here and that gives us just a little sliver that's in the corner that slice in this triangle here and now we can calculate each of these components for force C. So force C in the x-direction is force A, 385 newtons, minus 475 times sin 15 so I just substituted into this formula just now with numbers here and that works out to 262.06 newtons. And then force C in the y-direction is force B, 475 newtons, times cos 15 which is 458.81. So those are the two components for force C and then defined the hypotenuse... see what we figured out so far is, we found out that force C goes downwards this much, 458.81 newtons, and it goes to the right this much, F C x, 262.06 newtons that makes a right triangle with this resultant being the hypotenuse and we use Pythagoras to calculate it. So force C is the square root of F C x squared plus F C y squared so that's the square root of 262.06 newton squared plus 458.81 newton squared that gives 528.38. And then to figure out the angle and that is just the sliver in here, Θ C, that's the part between the vertical axis and the force so we are gonna have to add 90 to our answer here is gonna be the inverse tangent of the opposite which is F C x divided by the adjacent F C y. And that's inverse tangent of 262.06 divided by 458.81 newtons this gives 29.73. And we'll call that Θ or the answer that the question is looking for is the angle all the way from force A to force C so we'll just call that Θ and that's gonna be Θ C plus 90. So that's 90 plus 29.73, 129.73 should have three significant figures because you know the forces we were given are 385 and 475 and they had three significant figures so we'll have to round this to three significant figures which makes it into 130. So our final answer is the force C is 528 newtons, 130 degrees and then we have to say how this angle is measured because it's not in standard position. If you just said 130 degrees and that's all you said then the assumption would have to be that it's in standard position going counter-clockwise from the positive x-axis which is not the case so we have to be specific and say that our angle is measured clockwise from force A.