
A scallop forces open its shell with an elastic material called abductin, whose Young’s modulus is about . If this piece of abductin is 3.0 mm thick and has a cross-sectional area of , how much potential energy does it store when compressed 1.0 mm?
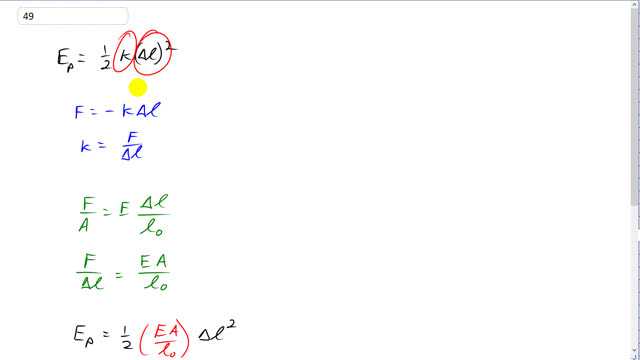
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. Elastic potential energy is one-half times Hooke's constant or the spring constant times the change in length of this elastic material, this abductin in this scallop, the change in length squared. Usually there's an x there, we usually write elastic potential energy is one-half kx squared but I mean you use a Δl just because that's what x represents: it represents the change in length. So to keep our units consistent between all the different formulas, let's try to keep the same letters everywhere. So we have Hooke's law says that the force is negative k times change in length or negative kx normally but we'll write negative k times Δl. And that means the spring constant is well negative I suppose but doesn't really matter, we just care about its magnitude. It's gonna be F divided by Δl. And then we turn our attention to the stuff from this chapter which says that the force applied to compress this material divided by its cross-sectional area equals its elastic modulus times the fractional change in its length, i.e., the change in its length divided by the original length. And we can rearrange this to write an expression of F divided by Δl by multiplying both sides by A over Δl. And then we are gonna create an expression for k that we can then substitute up here. And so the Δl's cancel here and the A's cancel here so we have F over Δl equals EA over l naught and this is useful because F over Δl is k. So now we can look at this equation again for elastic potential energy and write in one-half times EA over l naught instead of k times Δl squared. So we have one-half times 2.0 times 10 to the 6 newtons per square meter elastic modulus for this abductin times its cross-sectional area of 0.50 square centimeters which we have to multiply by 1 meter for every 100 centimeters squared in order to convert this into meter squared and divide by 3 millimeters expressed in meters 3.0 times 10 to the minus 3 meters and then times by the amount by which it's compressed which is 1.0 millimeters which we write as times 10 to the minus 3 meters and square that change in length and this gives 0.017 joules of elastic potential energy stored in the abductin.