
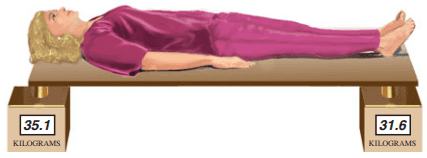
A 172-cm-tall person lies on a light (massless) board which is supported by two scales, one under the top of her head and one beneath the bottom of her feet (Fig. 9–64). The two scales read, respectively, 35.1 and 31.6 kg. What distance is the center of gravity of this person from the bottom of her feet?
In order to watch this solution you need to have a subscription.
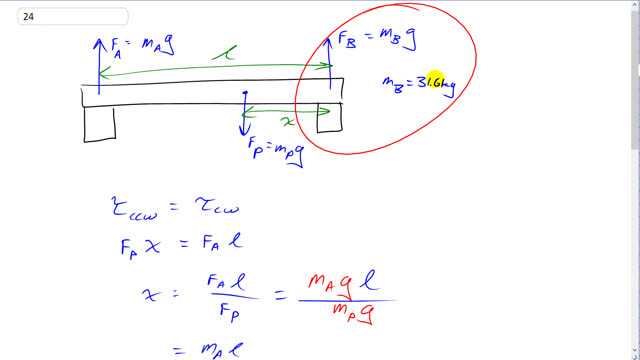
This is Giancoli Answers with Mr. Dychko. We have this scale at her feet which is registering a mass of 31.6 kilograms and we have another scale over at this person's head which is registering a mass of 35.1 kilograms and the question is where is this person's center of mass? And so it's somewhere here some distance x which we have to calculate from her feet and this is the weight of the person and that equals the mass of the person times g. And we'll take this to be the pivot point and we'll have the two torques then the one that's counter-clockwise is due to the person and it's their weight times the distance from the pivot x and that equals the clockwise torque due to force A—the scale under her head— which is mass A times g times its distance from the pivot which is the length l of this board that she's lying on. And we divide both sides here by F P— force of the person, their weight in other words— and x equals F A times l over F P and F A is the mass that the scale registers times g times l and that's divided by mass of the person times g and the g's cancel and we are left with m A l over m P. Now the problem with this equation is that we don't know what the mass of the person is so we'll turn our attention to this equation which is Newton's second law and it says that the total forces equals mass times acceleration but since there's no acceleration, another way to say it is all the forces add up together to make zero and the way I like to put it is the total force up has to equal the total force down. So we have all the forces up due to each of the scales A and B equals the total force down which is the weight of the person. So we have m Ag plus m Bg equals m P times g, g's cancel and you are left with mass of the person is m A plus m B so we can substitute that here as shown here. So we have x then is the mass of person A times the length of the board divided by the mass registered on both scales A and B added together and that gives about 90.5 centimeters from their feet; now the units are centimeters because we kept l in centimeters.