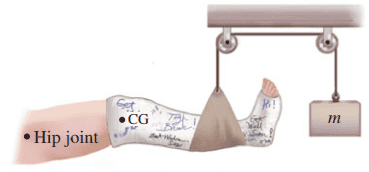
Calculate the mass $m$ needed in order to suspend the leg shown in Fig. 9–47. Assume the leg (with cast) has a mass of 15.0 kg, and its CG is 35.0 cm from the hip joint; the cord holding the sling is 78.0 cm from the hip joint.

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. The center of mass of the leg is positioned here a distance l 1 from the hip joint and results in some clockwise torque equal to the weight of the leg and mass of the leg m L times g times the lever arm l 1 so that's the clockwise torque. And then the mass that's hanging off via the pulleys over here— there's a mass hanging here— it results in a force applied upwards on the leg equal to the weight of the mass that's hanging down And so the force up here is gonna be mg— this is counter-clockwise torque on the leg— and the torque will be mg times its lever arm l 2 and we can divide both sides by g so it cancels and divide both sides by l 2 as well and we can solve for m— the mass that's hanging. And it's gonna be the mass of the leg 15 kilograms times the leg's lever arm 35.0 centimeters divided by the lever arm for the hanging mass like where that force is applied which is 78.0 centimeters from the hip joint. And notice that I did not convert these into meters; normally I would but in this case because we are dividing these two units they are gonna cancel anyway so it doesn't matter what the units are just so as long as they are the same units and we get an answer of 6.73 kilograms.