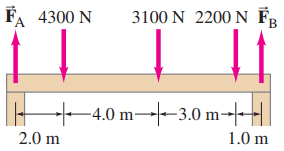
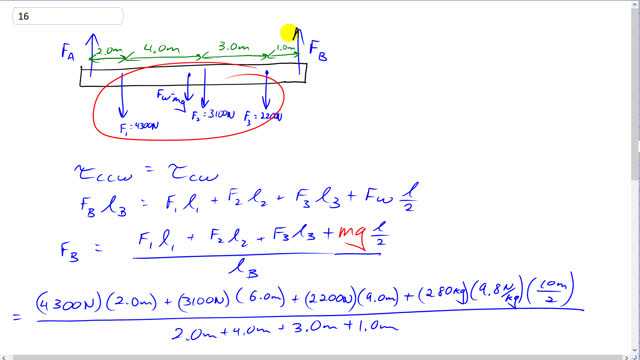
Calculate $F_A$ and $F_B$ for the beam shown in Fig. 9–56. The downward forces represent the weights of machinery on the beam. Assume the beam is uniform and has a mass of 280 kg

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. This beam is in equilibrium which means all the torques going clockwise— and there are four of them each due to these four forces— and then equals the torque going counter-clockwise and there's only one torque counter-clockwise which is due to F B going upwards this is all assuming that the pivot is over here at the position of F A. So we'll figure out F B by considering torque with this as the pivot over here at F A and so counter-clockwise is F B times the lever arm of this F B which is the total length of the beam and that equals the torque due to F 1 times its lever arm, 2 meters, plus F 2 times its lever arm which is 4 plus 2 meters which is 6 and then plus F 3 times its lever arm 3 plus 4 plus 2 which is 9 meters plus the weight of the beam which we assume is acting at the center of the beam, given that the beam has a uniform weight distribution or mass distribution, and so that's mg times the total length of the beam divided by 2 and the total length is 10 meters divided by 2. So we have 280 kilograms times 9.8 newtons per kilogram times 10 meters over 2 plus each of these forces multiplied by their respective lever arms divided by the total length of the beam which is the lever arm for the F B and then the calculator looks like this and we get about 6100 newtons must be F B. Now all the up forces have to equal all the down forces and so this is what we used to figure out F A, subtract F B from both sides and then substitute mg in place of F W for the weight of the beam and we get 4300 newtons plus 3100 newtons plus 2200 newtons plus the weight of the beam minus the answer for F B and we get 6300 newtons must be F A.