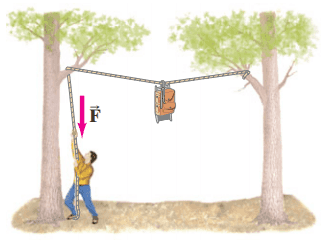
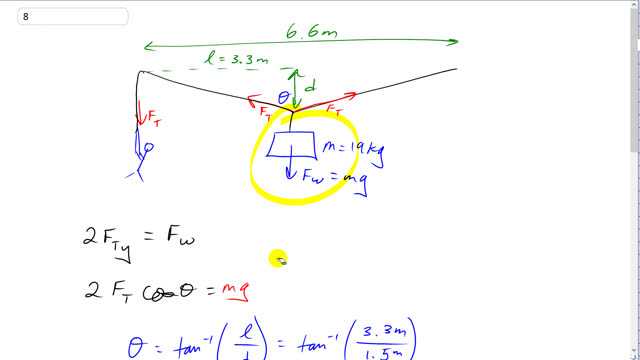
The two trees in Fig. 9–51 are 6.6 m apart. A backpacker is trying to lift his pack out of the reach of bears. Calculate the magnitude of the force $\vec{F}$ that he must exert downward to hold a 19-kg backpack so that the rope sags at its midpoint by

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. So we have a tree here and another tree here and the distance between them is 6.6 meters and the backpack is hanging in the middle of this rope and there's a force of tension along the rope going in this direction and in the other direction from this point where the backpack is hanging and tension along the rope is the same everywhere on the rope and so the force that the person pulls down with is the force of tension as well. And there's a y-component of this tension force which has to compensate for the weight pulling straight down so this y-component of this tension force is straight up and there are two of them: there's the y-component due to the tension force to the left and another y-component due to the tension force to the right and so that's 2 times the y-component of one of the tension forces has to equal the weight. And in the way I have drawn it here, we have Θ in this part of the triangle and that means that the y-component of the tension force will be F T times cos Θ because the y-component is the adjacent to this angle Θ here and we have 2F Tcos Θ equals mg, the weight of the backpack. And we need to figure out what Θ is then: it's the inverse tangent of the distance from the midpoint to the tree so that's half of the total distance between the tree, half of 6.6 is 3.3 and that divided by the amount by which the backpack is sagging— so 1.5 meters in part (a)— so that gives an angle of 65.556. And so we take 19 kilograms times 9.8 newtons per kilogram times 2 times cos of 65.556 and that gives about 220 newtons. Now if the person is really concerned about a tall bear and they want their backpack to be even higher and have it sag by only 0.15 meters then the angle Θ is gonna be different and that's what we'll calculate here. So that's 3.3 meters same distance between the midpoint of the rope to the tree but now divided by only 0.15 meters and that gives 87.397 degrees and we take 19 kilograms times 9.8 newtons per kilogram divided by 2 times cos 87.397 and we get about 2.0 times 10 to the 3 newtons when we round this to two significant figures.