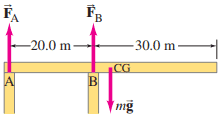
Calculate $F_A$ and $F_B$ for the uniform cantilever shown in Fig. 9–9 whose mass is 1200 kg.

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. The total torques about any pivot that we choose has to equal zero and the total up forces have to equal total down forces and that's true for any static's question. So let's consider our pivot to be at support A in which case there are two torques: there's the counter-clockwise torque due to force B which exerts a torque in that direction and then there's a clockwise torque due to the weight of the beam. And since the beam is uniform, we can consider this weight to be acting at the center of the beam. So the counter-clockwise torque is F B times its lever arm B which is 20 meters from support A and that equals the clockwise torque which is the weight times its lever arm which is the total length of the beam which is 20 plus 30 which is 50 meters divided by 2 and so force B is mgl divided by l B times 2. So it's 1200 kilograms—mass of the beam— times 9.8 newtons per kilogram times 50 meters divided by 20 meters— lever arm of the beam—times 2 and that gives about 1.5 times 10 to the 4 newtons must be the force due to the support B. Now the total up forces, F A plus F B, has to equal the total down forces, mg. So F A is mg minus F B when we subtract F B from both sides. So that's 1200 kilograms times 9.8 newtons per kilogram minus 14700 newtons that we discovered up here and this works out to negative 2900 newtons which means the force is down—that's what the negative sign means— so there must be some bolts attaching this beam to the support in order for the support to exert a force downwards. So the force actually is pointing this way, that's force A. But the fact that we guessed wrong here is fine; our answer worked out to be negative and so that tells us what the correct direction is: downwards.