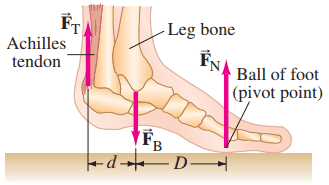
The Achilles tendon is attached to the rear of the foot as shown in Fig. 9–73. When a person elevates himself just barely off the floor on the “ball of one foot,” estimate the tension $F_T$ in the Achilles tendon (pulling upward), and the (downward) force $F_B$ exerted by the lower leg bone on the foot. Assume the person has a mass of 72 kg and $D$ is twice as long as $d$.

VIDEO TRANSCRIPT

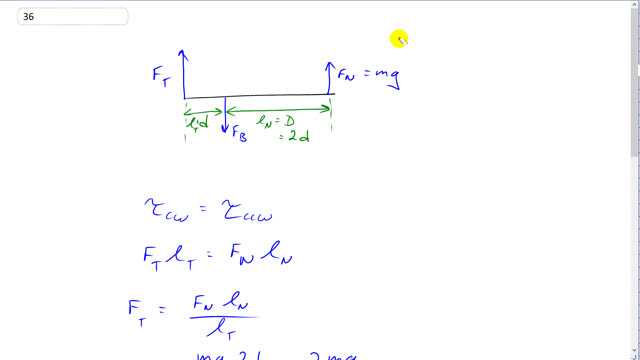
This is Giancoli Answers with Mr. Dychko. When the foot just barely starts to rise off the ground or the heel rises off the ground that means the ball of the foot is the only part in contact with the ground and so the normal force exerted upwards on the ball of the foot has to be equal to the weight of the person. So we know what this normal force is and we don't know what this force of the Achilles tendon upwards is. And we also don't know the force of the bone pushing down the foot here so let's take our pivot to be at this point and then F B will not enter into our torque equation because it will have no lever arm. So we have the clockwise torque due to the tendon F T times the lever arm of the tendon— distance from the pivot— equals the normal force times its distance from the pivot and we can divide both sides by l T and we get the tendon force is the normal force times normal force lever arm divided by lever arm of the tendon. The normal force is mg and then the lever arm for the normal force is 2 times d, we are told, and then that's divided by lever arm of the tendon, which is d, and little d's cancel giving us 2mg is the Achilles tendon force. So Achilles tendon force is 2 times the person's weight: 2 times 72 kilograms times 9.8 newtons per kilogram which is 1400 newtons. And then all the down forces have to equal the total up forces so we have the force exerted by the bone on the foot downwards has to equal the tendon force up plus the normal force up. So that's 2mg is the tendon force plus the weight of the person normal force mg and that's 3mg so 3 times 72 times 9.8 gives 2100 newtons.