
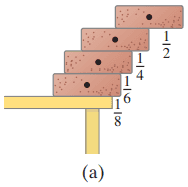
Four bricks are to be stacked at the edge of a table, each brick overhanging the one below it, so that the top brick extends as far as possible beyond the edge of the table.
- To achieve this, show that successive bricks must extend no more than (starting at the top) , , , and of their length beyond the one below (Fig. 9–75a).
- Is the top brick completely beyond the base?
- Determine a general formula for the maximum total distance spanned by bricks if they are to remain stable.
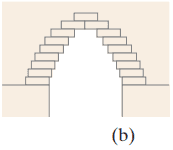
- A builder wants to construct a corbeled arch (Fig. 9–75b) based on the principle of stability discussed in (a) and (c) above. What minimum number of bricks, each 0.30 m long and uniform, is needed if the arch is to span 1.0 m?
- see video
- yes, the top brick is completely beyond the edge of the table
- 35 bricks (see the spreadsheet in the video for the numerical solution and explanation)
In order to watch this solution you need to have a subscription.
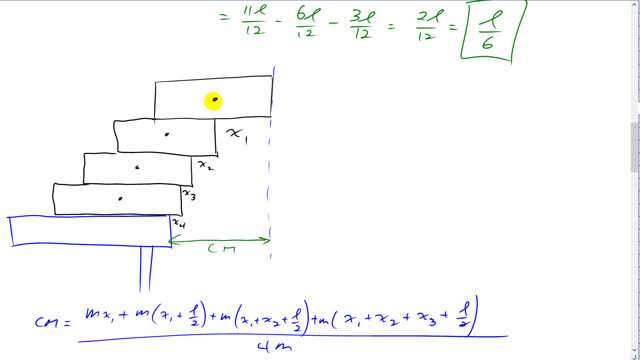
This is Giancoli Answers with Mr. Dychko. We are going to talk about our corbelled arch in this question and it's kind of interesting because it's counter-intuitive in that you will notice that this top block can actually extend beyond the edge of the table entirely to the point where this left edge of this top block is off beyond the edge of the table and it shows you how some of these arches of medieval type architecture can be built. And first we'll show that this distance x 1 between the edge of the block and the table is gonna be equal to the block's length divided by 2 And well I'm not really gonna show much in this case because it's pretty clear that since the block is uniform, we know the center of mass has to be above the pivot and so the center of mass will be in the center of the block in which case x 1 is gonna be the block's length divided by 2. Now for this second part, it gets a little bit more involved; we'll take this to be our reference position, our x equals zero point this right edge of the top block and we'll find the center of mass of the system by going one mass multiplied by the distance from the center of mass to a reference point and then plus the other mass times its distance from its center of mass to our reference point and then divide by the total mass. And then after we get this position of this center of mass, we'll figure out what x 2 is by going center of mass minus x 1. So center of mass minus x 1 will give us x 2. So we have m times x 1 is the distance from this center of mass of the block to the reference point and then plus this mass which is also m— no need for subscripts, all the blocks are the same mass— times a distance of x 1 plus an additional l over 2 half the length of the block to get from the center of mass of this bottom block to the edge here and that's this distance here and all that gets divided by the total mass which is 2m. And then multiply both sides by 2 and cancel away the m's and you get 2 times the center of mass length equals x 1 plus x 1 plus l over 2. Now x 1 we have calculated already is l over 2 so making that substitution and we have 3l over 2 on the right side and divide both sides by 2 and you get center of mass is at a distance 3l over 4 from the edge of the table to the right edge of the top block. So x over 2 is the center of mass minus x 1 and that's gonna be 3l over 4 minus l over 2 which is 3l over 4 minus 2l over 4 which is l over 4, x 2 is l over 4. Then when you have three blocks, the center of mass is at this top mass times its distance from our reference point which is still m times x 1 plus the middle block mass m times its distance of mid center of mass to this dotted blue line which is x 1 plus half the block length l over 2. And then plus the distance from this center of mass to the dotted blue line which is x 1 plus an additional x 2 plus l over 2, half of block length and all that gets divided by 3 times m. So you cancel the m's again and multiply both sides by 3 and you get 3 times the center of mass length is l over 2, substituting for x 1 plus l over 2 again plus l over 2 copied plus l over 2 for x 1 plus l over 4 for x 2 plus this l over 2 here. It gives us a total of one, two, three, four, five l over 2's plus this l over 4 here and common denominator will be 4 so multiply top and bottom by 2 that's 10l over 4 plus l over 4 which is 11l over 4 and divide both sides by 3 and you get center of mass is at 11l over 12 so this is 11l over 12 that total distance. So to find x 3, take that total distance 11l over 12 and subtract away x 1 and subtract away x 2 as well. So we subtract away l over 2 for x 1 and l over 4 for x 2 and you get, well, the common denominator is gonna be 12 here so it's top and bottom by 6 on this one and top and bottom multiply by 3 here so that's 11l over 12 minus 6l over 12 minus 3l over 12 which is 11 minus 9 which is 2l over 12 which is l over 6 in reduced form. There so x 3 is l over 6. And lastly, we'll show that x over 4 or x 4 turns out to be l over 8. So it's the same process, just takes longer now. We have this mass times this distance from the reference point of x 1 and then plus this mass times its distance from the reference point x 1 plus half a block length l over 2 plus this mass here times its distance from the reference point of x 1 plus x 2 plus half a block length and then plus this very bottom mass times this distance from the reference point of x 1 plus x 2 plus x 3 plus half a block length and all that gets divided by the total mass of 4m. Cancel the masses, multiply both sides by 4 and then substitute for x 2 and x 3 and x 1 and we get l over 2 plus l over 2 plus l over 2 plus this x 1 becomes l over 2 plus this x 2 becomes l over 4 plus this l over 2 is copied plus l over 2 plus l over 4 plus l over 6 in place of x 3 plus l over 2 and there's 7l over 2's and then there's 2l over 4's plus a single l over 6 and a common denominator can be 6 here and well you can reduce this to l over 2 which becomes and then multiply both sides by or top and bottom by 3 over 2 you can put it that way and it becomes 3l over 6 and 21l over 6 plus l over 6 makes 25l over 6 and that's the distance from this reference point right edge of the top block to the table edge and x 4 is gonna be that center of mass distance minus x 1 minus x 2 minus x 3. So that all works out when you have a common denominator 24 to 3l over 24 which is l over 8. So in part (b), it asks us will this top block be entirely clear of the edge of the table and the answer is yes it will because this center of mass distance between the right edge of the top block to the edge of the table is 25l over 24 which is more than l and so this is gonna be 124thl away from the edge of the table there to the right side of it. And then the general formula for the total distance covered by this half an arch is gonna be the sum of the length of one block over 2 times i where this expands into a series; we can also factor out the l there if you like. So it factors out and turns into a series of l times 1 over 2 plus 1 over 2 times 2 plus 1 over 2 times 3 plus 1 over 2 times 4 plus 1 over 2 times 5 and so on and that can be written more concisely with this using sigma notation where n is the number of blocks in total. Okay. And if you had to cover a total span of 1 meter, the solution to this equation here is it can only be done numerically so that's probably unusual. Typically, you can solve your equations by just, you know, solving for the unknown and plugging into a calculator to get an answer but it doesn't work like that in this case. You have to use a spreadsheet or something like it or guess and check and and I'm using a spreadsheet here—this is LibreOffice and anything will do, Microsoft Excel or whatever you have— and let's see. We have number of bricks on one side and we have the span that that half arch will cover and this is an equation in this cell referring to the result from the cell before it 'B2' plus 0.3 since that's the length of one of the blocks, one of the bricks times one-half times 1 over this number here. That's 'A3' is referring to this number here. And so and so on, you can take the bottom right corner of this cell and then drag it down and the formula gets copied and it automatically advances this index here 'A7' becomes 'A8' and so on. So this is a recursive formula because it's referring to the result of the previous iteration. So to get the full span of the arch and multiply that result in column 'B' by 2 and we can see that we finally span a full meter when we have sixteen blocks on one side so this is the number of blocks in one side. So there would be 32 blocks in total on both sides of the arch. Now according to the picture the way a corbelled arch is constructed, there's gonna be one block here and another block here on the bottom that will have their edge flush with the base and so those are not included in our work here. So we have to add them— 2 on the bottom— and then there's 1 block stuck on top and that's additional as well. So we have a total of 2 times 16 which is 32 plus 3 is 35 bricks to make this corbelled arch.