A uniform ladder of mass $m$ and length $l$ leans at an angle $\theta$ against a frictionless wall, Fig. 9–70. If the coefficient of static friction between the ladder and the ground is $\mu_s$, determine a formula for the minimum angle at which the ladder will not slip.

VIDEO TRANSCRIPT

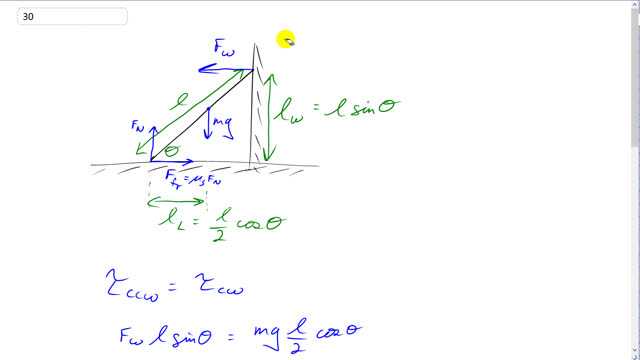
This is Giancoli Answers with Mr. Dychko. Since this wall is frictionless that means its force is entirely horizontal, there's no vertical component to it. So here's the force of the wall going straight to the left and to figure out the torque due to this wall force, we'll multiply it by the perpendicular distance to the pivot which we'll take to be here at this point of contact with the ground. And so the position vector linking this the point where the wall force is applied to the pivot is on this red line and we'll take the component of that which is perpendicular to the force. So we have l—length of the ladder— times sin of Θ to get l w—lever arm for the wall force. And then we wanna figure out the torque due to the weight of the ladder so we'll take mg—the force downwards— and multiply that by the component of the position vector linking the center of gravity to the pivot, this is of length l over 2 and we'll take the component of that perpendicular to the weight. So the horizontal component is l subscript L—for ladder— and that's l over 2 times cos Θ this being the adjacent leg of this triangle here. And then we'll say that counter-clockwise torque equals clockwise torque so the counter-clockwise torque is F w times lsin Θ and that equals mg times l over 2 cos Θ and sin Θ divided by cos Θ is, after you cancel the l's, mg over 2F w where I divided both sides by F w and divided both sides by cos Θ and divided both sides by l too. And sin Θ over cos Θ you have to memorize is tan Θ— that's a trigonometric identity— so tan Θ is mg over 2F w. And that would answer our question if we knew what F w was but we don't know what it is so let's work on that. Horizontal forces have to balance here so the wall force to the left has to be balanced by this static friction force at this contact with the ground which acts to the right and it will have a maximum of μ S times F N— the coefficient of static friction times the normal force— and the normal force upwards has to balance all of the forces going downwards of which there's only one— the weight of the ladder—so the normal force equals mg in this case so we'll make that substitution. So the wall force in the end equals the static friction coefficient times mg. So we'll substitute that in for F w here and the mg's will cancel leaving us with tan Θ is 1 over 2μ S. And so Θ, the minimum angle that's possible, was gonna be the inverse tangent of 1 over 2 times the coefficient of static friction.