
Giancoli's Physics: Principles with Applications, 7th Edition
9
Static Equilibrium; Elasticity and Fracture
Change chapter9-1 and 9-2: Equilibrium
9-3: Muscles and Joints
9-4: Stability and Balance
9-5: Elasticity; Stress and Strain
9-6: Fracture
9-7: Arches and Domes
Question by Giancoli, Douglas C., Physics: Principles with Applications, 7th Ed., ©2014, Reprinted by permission of Pearson Education Inc., New York.
Problem 50
Q
The femur bone in the human leg has a minimum effective cross section of about . How much compressive force can it withstand before breaking?
A
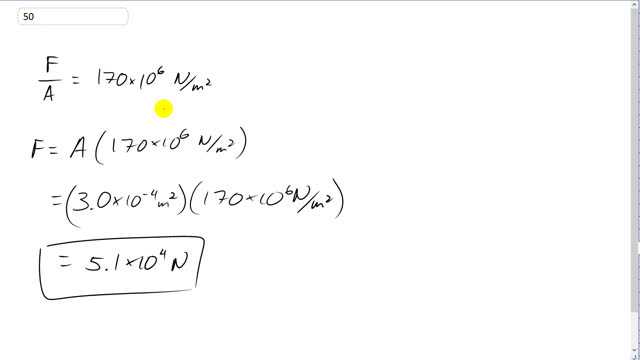
In order to watch this solution you need to have a subscription.
VIDEO TRANSCRIPT
This is Giancoli Answers with Mr. Dychko. The maximum compressive stress that bone can withstand is 170 times 10 to the 6 newtons per square meter which we get from table [9-2] on page 245 and that equals force over area because stress is force divided by cross-sectional area. So we multiply both sides by A and then we get F is A times that compressive strength. And so area is 3.0 times 10 to the minus 4 square meters times 170 times 10 to the 6 newtons per square meter and you get 5.1 times 10 to the 4 newtons.
Giancoli Answers, including solutions and videos, is copyright © 2009-2025 Shaun Dychko, Vancouver, BC, Canada. Giancoli Answers is not affiliated with the textbook publisher. Book covers, titles, and author names appear for reference purposes only and are the property of their respective owners. Giancoli Answers is your best source for the 7th and 6th edition Giancoli physics solutions.