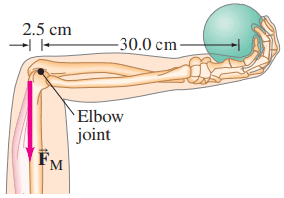
Approximately what magnitude force, $F_M$, must the extensor muscle in the upper arm exert on the lower arm to hold a 7.3-kg shot put (Fig. 9–71)? Assume the lower arm has a mass of 2.3 kg and its CG is 12.0 cm from the elbow-joint pivot.

VIDEO TRANSCRIPT

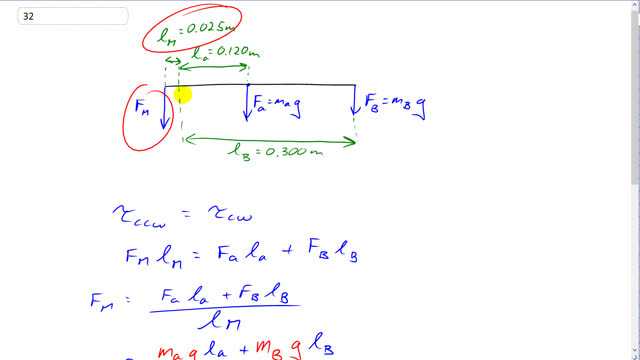
This is Giancoli Answers with Mr. Dychko. The lever arm of the extensor muscle is 0.025 meters when you convert 2.5 centimeters into meters and that's how far it is from this elbow joint and this elbow joint is gonna be the pivot that we calculate all the torque's about. So the center of mass of the arm is 0.120 meters from that pivot and so it has a torque of l a— lever arm for the arm— multiplied by F a—the weight of the arm— and then the ball exerts a clockwise torque equal to the weight of the ball F B times the lever arm of the ball which is 0.300 meters 30 centimeters away from the elbow pivot and the counter-clockwise torque is force of the muscle times its lever arm and we solve for the force of the muscle by dividing both sides by l M it cancels on the left and ends up on the right hand side and then substitute for force of the arm and force of the ball they are two weights m ag and m Bg respectively and factor out the common factor g and you have the force of the muscle is g times mass of the arm times lever arm of the arm plus mass of the ball times lever arm of the ball divided by lever arm of the muscle. And plug that into your calculator: 9.8 newtons per kilogram times 2.3 kilograms—mass of the arm— times 0.120 meters plus 7.3 kilograms—mass of the ball— times its lever arm of 0.300 meters divided by 0.025 meters— lever arm of the muscle— and that gives about 970 newtons.