A 110-kg horizontal beam is supported at each end. A 320-kg piano rests a quarter of the way from one end. What is the vertical force on each of the supports?

VIDEO TRANSCRIPT

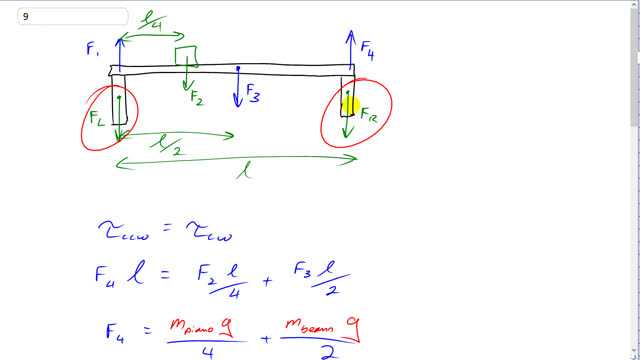
This is Giancoli Answers with Mr. Dychko. We need to figure out the forces on the two supports here: here's the support on the right and the support on the left. So it has force exerted F R on the right support and F L down on the left support and we are gonna use though this force here in our calculations for the force exerted on the horizontal beam due to the support here and that's the Newton's third law counterpart to the force that's on the support. So I could rewrite the subscripts to illustrate that better: I could say this is the force on the right hand support due to force 4 and this force here is the force... maybe we'll say it this way, let's use subscripts for the objects. So this is the force on the right hand support due to the beam—that's this one— and this is the force on the beam due to the right hand support and because they have the same subscripts in the opposite order that means that they are Newton's third law counterparts or Newton's third law pairs. So the force on the right hand support due to the beam, which is what we have to find, is gonna be the negative of the force on the beam due to the right hand support. And we are gonna involve this force because that's gonna enter into our torque equations and everything else that we are gonna deal with when we talk just about the beam so let's get to work on that. If we talk about torque, we say that the counter-clockwise torque about the pivot which we'll choose to be at the left side equals the clockwise torque about the same pivot and so force 4 is responsible for the counter-clockwise torque and so it gets multiplied by the distance l from the pivot and that equals the torque due to the piano F 2 downwards times its distance from the pivot the full length divided by 4 because we are told it's a quarter of the ways from one end plus force 3 which is the weight of the beam times its lever arm which is the beam length divided by 2 since we assume that the beam is uniform distribution of mass along the beam and so that would put its center of gravity in the geometric center of the beam l over 2. And we can divide everything by l— beam length doesn't matter— and force 4 then is gonna be the weight of the piano— mass of piano times g— over 4 plus the weight of the beam and beam times g over 2 and factor out the g over 2 and you get this and you don't have to do that factoring out if you don't want to but it just makes it a little cleaner I think. And then we have 9.8 newtons per kilogram divided by 2 times 320 kilograms—mass of the piano—divided by 2 plus 110 kilograms—mass of the beam— and that works out to about 1300 newtons. That's the force 4 and it's positive and it's upwards which would make F R equal magnitude but opposite direction so F R or the force on the right hand support is 1300 newtons down. And then we need to figure out force 1 which did not enter into our torque equation because force 1 exert no torque about this pivot here since it has no lever arm. And so we'll use this by saying all the up forces have to equal all the down forces; this is the same as saying Newton's second law which is that the sum of all forces equals mass times acceleration where acceleration is zero here so all forces added together make zero and you can also say all the up forces act equal to all down forces. (There's a mistake in there with the subscripts.) So F 1 and 4 are up and F 2 and 3 are down. So this is 2 and this is 3; 2 is the piano and 3 is the beam. Okay so F 1 is F 2 plus F 3 minus F 4 so that's the weight of the piano down plus the weight of the beam down minus the force 4 upwards and this works out to 320 kilograms times 9.8 newtons per kilogram plus 110 kilograms times 9.8 newtons per kilogram minus 1323 newtons—which we figured out before and notice I'm using the unrounded answer to avoid intermediate rounding error— and we get about 2900 newtons and that means the force on the left hand beam downwards is gonna be equal to force 1 upwards just in the opposite direction. So that's gonna be 2900 newtons down.