You are here

Select a problem

Question:

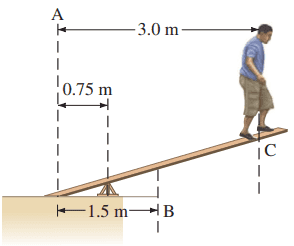
You are on a pirate ship and being forced to walk the plank (Fig. 9–68). You are standing at the point marked C. The plank is nailed onto the deck at point A, and rests on the support 0.75 m away from A. The center of mass of the uniform plank is located at point B. Your mass is 65 kg and the mass of the plank is 45 kg. What is the minimum downward force the nails must exert on the plank to hold it in place?

Problem 28.

Problem 9-68.

Giancoli, Douglas C., Physics: Principles with Applications, 7th Ed., ©2014. Reprinted by permission of Pearson Education Inc., New York.
The question will be visible after logging in, as required by Pearson Education Inc.

Quick Answer:

$2.4 \times 10^3 \textrm{ N}$

Giancoli 7th Edition, Chapter 9, Problem 28

(2:40)

Chapter 9, Problem 28 is solved.

View sample solution

Transcript for this Giancoli solution

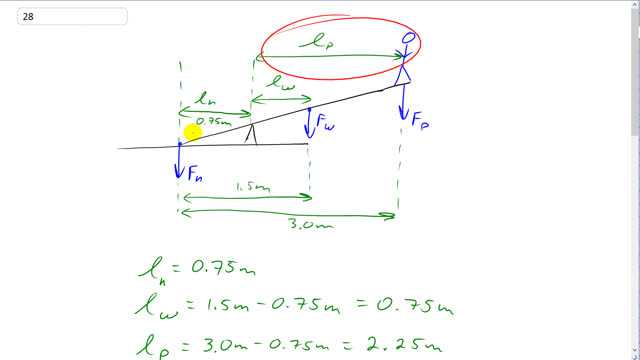
This is Giancoli Answers with Mr. Dychko. One thing that's convenient about this question is that they have given us all these distances perpendicular to the forces so there's no need to do any trigonometry we don't care what this angle is in here. So this question is actually a little bit easier than it looks. We are gonna, you know, use torque to answer our question as to what this nail force downwards has to be and we need to multiply this person's weight straight down by their distance from the pivot which we'll take to be this point here. That's l P—lever arm for the person— and then another clockwise torque will be the weight of the plank multiplied by its lever arm l W— distance from the pivot— and then we'll take the nail force times the lever arm for the nail to be the counter-clockwise torque. And l n for the nail is given to us in the diagram 0.75 meters and the lever arm for the person's or the plank's weight is gonna be the one and the half meters here subtract the distance from the pivot to the nails so that's 1.5 minus 0.75 which is 0.75 and the lever arm for the person will be the full 3 meter distance from the nail to this point here where the person is and minus the lever arm of the nail. so that's 3 minus 0.75 which is 2.25. So the counter-clockwise torque—force of the nail times the lever arm of the nail— that equals the total clockwise torque the plank weight times the length of the plank lever arm plus the force of the person which is their weight times their distance from the pivot. Divide both sides by l n and you get F n is F wl w plus F pl pdivided by l n and then substitute for those weights so this is the mass of the plank times g this is the mass of the person times g... 'w' is a bit of a weird subscript but I can't use 'p' for plank because that would be confusing with p for person here, factor out the g and you get g times all that and we have 9.8 newtons per kilogram times 45 kilograms—mass of the plank— times 0.75 meters plus 65 kilograms— mass of the person— times 2.25 meters all divided by 0.75 which is 2.4 times 10 to the 3 newtons.

Comments

By leopinzon18 on Sat, 11/05/2016 - 10:02

what formulas are being used

By Mr. Dychko on Tue, 11/08/2016 - 00:42

Hi leopinzon18, for formulas being used are $\tau = Fl_{\bot}$ which says torque equals force times the perpendicular component of the lever arm, and the other formula is that $\Sigma \tau = 0$ for static equilibrium, which is also to say $\Sigma \tau_{ccw} = \Sigma \tau_{cw}$ meaning the counter-clockwise torques equal the clockwise torques. If you have a more specific question, just let me know and I'll see if I can answer it.

Best,
Mr. Dychko