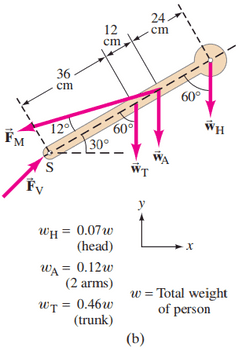
Redo Example 9–9, assuming now that the person is less bent over so that the $30 ^\circ$ in Fig. 9–14b is instead $45 ^\circ$. What will be the magnitude of $F_V$ on the vertebra?

VIDEO TRANSCRIPT

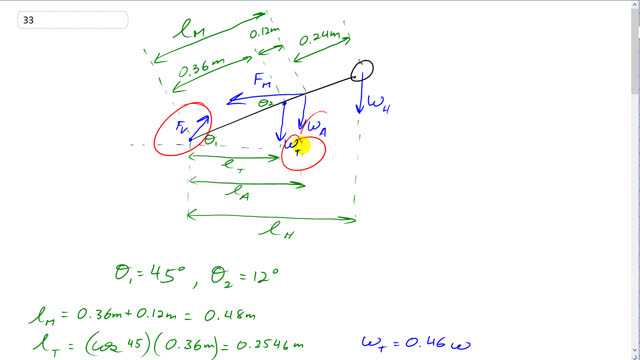
This is Giancoli Answers with Mr. Dychko. We are going to find the force on the bottom vertebrae in a person's back and we know the weight of their trunk, the weight of their arms and the weight of their head and those are all given to us in the figure [9-14] and that's these things here. So weight of their trunk is 0.46 times their total body weight, weight of the arms is 0.12w and weight of the head is 0.07 times w and each of these weights has to get multiplied by lever arm which is the perpendicular distance to the pivot which we'll take to be at the bottom here where the vertebrae force is acting and by doing that, we make sure that F v does not appear in our torque equation and so that means the only unknown we'll have is this force due to the back muscles that are keeping the person in this 45 degree bent-over position. And after we figure out this F M, we'll know all the forces except for F V which we can then figure out using all the up forces have to equal the down forces and all the forces to the left have to equal all the forces to the right. So first is torque then. So for each of these weights, it's fairly straightforward we find the lever arm of the trunk and it's gonna be this distance perpendicular to the force to the pivot so l T and it's gonna be cos of Θ 1 which is 45 degrees multiplied by the hypotenuse which is 0.36 meters. So lever arm for the trunk is cos 45 times 0.36 which is 0.2546 meters and for the arm, it's the same idea: it's this distance here which is 0.36 plus 0.12 which is 0.48 multiplied by cos 45 giving us 0.3394 meters. And then for the head, the perpendicular distance from where the force is acting to the pivot is this total length of the body multiplied by cos 45 so it's 0.72 meters times cos 45 or 0.5091 meters. And then when we are talking about the force due to the muscles, we are going to take the lever arm to be the distance along the body— 0.48 meters—and then multiply that by the perpendicular component of the muscle force so that's this part here. So I'm actually doing two strategies here: when it comes to dealing with the weights, I'm resolving the position vector into its perpendicular component and then when it comes to the back muscle force, I'm taking the position vector as is and taking the force and finding its component perpendicular to the position and either way is fine just as long as you have to make sure that the distance and the forces are perpendicular and you can resolve whichever one into the component that works. So taking the perpendicular component of the force here whereas with the weights, I'm taking the perpendicular component of the position. And the perpendicular component of the muscle force is gonna be the muscle force multiplied by the sin of Θ 2 because this is the opposite leg of that triangle here so we sin of 12 degrees which is Θ 2 multiplied by the muscle force to get that perpendicular component of the force. So that's F M times sin 12 times lever arm of the muscle equals the trunk weight times its lever arm plus the arm weight times its lever arm plus the head weight times the head's lever arm. So substituting F Msin 12 for F M ⊥ equals this same thing repeated and then divide both sides by sin 12 times l M and you end up with F M equals this whole thing divided by sin 12 l M and then substitute in a bunch of numbers. So we have 0.46 times w for the trunk weight times 0.2546 meters—trunk lever arm— plus 0.12w for the arm weight times 0.3394 meters which is the arm's lever arm plus 0.07w for the weight of the head times 0.5091 meters for the lever arm of the head divided by sin 12 times 0.48 meters and that gives the muscle force of 1.9387 times w. So the question is what is the vertebrae force? Well, the x-component of it is gonna equal the x-component of the force due to the muscle and that's because all the other forces are vertical and so the only force to the left is the component of the muscle force which is acting to the left and so that's gonna equal the vertebrae force to the right. Now to calculate this component of the muscle force, we need to look at this picture. So here's the body drawn again and here's the 12 degrees between the body and the muscle force and this dotted line is in the x-axis and it's parallel to this dotted line and this angle here, 45 degrees, is equal to this total angle here between the dotted line and the body— these are interior opposite angles— and that means that Φ which is this part that's up here that we are interested in plus 12 degrees equals 45 and so Φ is 45 minus Θ 2 which is 12 so 45 minus 12 is 33 degrees and the reason that's interesting is because the horizontal component of this muscle force this is F M x, it's gonna be F M times cos of Φ because this is the adjacent leg of this triangle here and we have F M y straight down which is what we are gonna deal with in a minute in the next step right here. So F M x is F M cos Φ so that's 1.9387w times cos 33 which is 1.6260w—that's the x-component of the vertebrae force. And then the y-component, well, it's the only force upwards is a y-component of this vertebrae force and that has to equal all of the other y forces downwards. So that's the three weights plus the component of the muscle force which is down. So the component of the muscle force down is the muscle force times sin of 33, sin of Φ, and you have 0.46w plus 0.12w plus 0.07w plus all that and that gives 1.7059w. So now that we have the components, we can use Pythagoras to find the resultant magnitude of the vertebrae force. So that's the square root of the sum of the squares of the components of the vertebrae force. So that's square root of 1.626w squared plus 1.7059w squared the w squared factors out into w and these numbers work out to 2.3525 which we'll round to 2.4. So the vertebrae force is 2.4w which is slightly less than when the person was bent over 30 degrees. So by standing more upright, there's less force exerted on the back muscles or sorry, I should say on the vetebrae, there!