How high must a pointed arch be if it is to span a space 8.0 m wide and exert one-third the horizontal force at its base that a round arch would?

VIDEO TRANSCRIPT

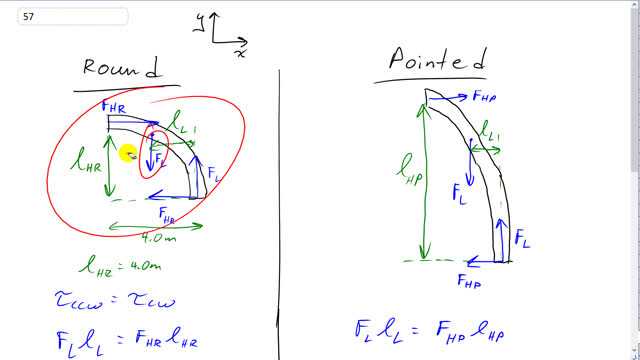
This is Giancoli Answers with Mr. Dychko. Let's consider half of each arch: the reason that this half an arch doesn't fall over when it has this load force on it pushing it down is because there's a horizontal force being applied to the right here by the the other half of the arch that's standing over on this left side so the right side is being pushed over to the right by this section of arch on the left. And this force that the left hand section of arch applies results in a torque with a lever arm equal to— l H for horizontal, R for round arch case— this lever arm, it's this perpendicular distance from the point where this force is applied to the pivot which we'll take to be at the base of the arch and that's gonna be the clockwise torque. And the counter-clockwise torque is this load force which is some distance—who knows— from the pivot that perpendicular distance anyhow. So that's l for lever arm subscript L for load and these two torques have to be equal to each other for static equilibrium and we have then that the load force times the load lever arm equals the horizontal force for the round arch times the lever arm for the horizontal force in the round arch. Okay. Now since this arch is round, well, we know what this l HR is because we are told that this arch has to span a total of 8 meters so from base to base, it's 8 meters and so for half the arch as we have shown here, the distance from the base to the halfway point is gonna be 4 meters and because it is round that means the distance from the bottom here to the top is gonna be 4 meters as well— it's a circle— so this is the radius, this l HR. For the pointed arch however, this lever arm is not gonna be 4 and we have to calculate what it should be such that this force exerted horizontally on the base is one-third the force here. I guess I should also mention that we are concerned with this force here because the horizontal force on the base, which is actually what we have to find, is gonna have equal magnitude to the horizontal force applied on the top of the arch to the right because that has to be balanced by something and that something will be this force horizontally to the left on the base. So when we solve for this, we are also solving for this. There's also a force vertical on the base to balance the load force downwards but this particular force is not what we are interested in. So for the pointed arch, it's the same kind of story: we'll take this load force to be the same distance from the base as we did for the round arch case because you know, there's nothing changing about this load on top I mean I guess... we have taken out a section of wall from here to here to make this higher arch but let's not be too picky about that. So same load force say, same distance from the base and there's now gonna be a horizontal force for the pointed arch to the right and it's gonna have a lever arm l horizontal pointed, l HP for this pointed arch and this lever arm is gonna be greater. And otherwise same idea: calculate the torque's, set them equal to each other so we have a load force times the load lever arm equals the horizontal force for the pointed arch times the lever arm for the horizontal pointed arch force. And we are told that the horizontal force on the base for the pointed arch has to be one-third the horizontal force on the base for the round arch and we can do a bit of algebra here to solve for F HR and it equals F L times lever arm for the load divided by the lever arm for the horizontal force in this round case. And now since F HP is one-third F HR, we'll substitute here and we'll write one-third times F HR and F HR being this, we have F L times l L divided by l HR and that equals, well, you end up with this here and the F L times lever arm of the load cancels on both sides and so you are left with 1 equals l HP divided by 3l HR. And then multiply both sides by 3l HR and you end up with l HP equals 3 times the lever arm for the horizontal force in the round case. So that's 3 times 4.0 meters and that gives 12 meters. So the arch has to be 12 meters high in order for the horizontal force in the base to be one-third what it was for the round arch.