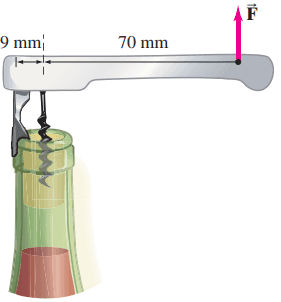
The force required to pull the cork out of the top of a wine bottle is in the range of 200 to 400 N. What range of forces $F$ is required to open a wine bottle with the bottle opener shown in Fig. 9–55?

VIDEO TRANSCRIPT

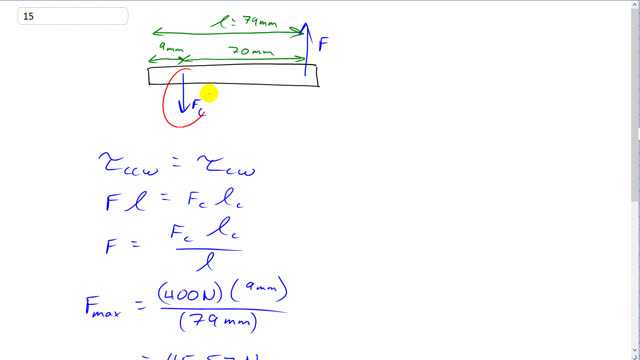
This is Giancoli Answers with Mr. Dychko. The force required to pull the cork out of the bottle is the same as the force that the cork exerts on the bottle opener downwards. So we have... this is gonna be between 400 newtons and 200 newtons and here's the force F that's supplied by the hand upwards on the corkscrew. Now we know that the torques are gonna be the same just at this point where it just begins to move and so the torque counter-clockwise equals the torque clockwise. So the force times the lever arm which is 79 millimeters because it's 70 millimeters from the screw and then a further 9 millimeters from the pivot at the edge of the bottle and that is gonna equal the force of the cork times its lever arm which is just the lever arm of the cork which is only 9 millimeters and divide both sides by l to solve for the force upwards that's applied. So that will be at most 400 newtons times 9 millimeters divided by 79 millimeters— these units don't have to be meters, they just have to be the same that's the only thing that's important so that they cancel— and we end up with 45.57 newtons and at a minimum, the force applied will be the 200 newtons that the force that the cork needs to experience times 9 millimeters divided by 79 millimeters which is only 22.78. So the force applied will vary somewhere between 50 newtons and 20 newtons with only one significant figure since this distance 9 millimeter has only one significant figure.