
The Leaning Tower of Pisa is 55 m tall and about 7.7 m in radius. The top is 4.5 m off center. Is the tower in stable equilibrium? If so, how much farther can it lean before it becomes unstable? Assume the tower is of uniform composition.
In order to watch this solution you need to have a subscription.
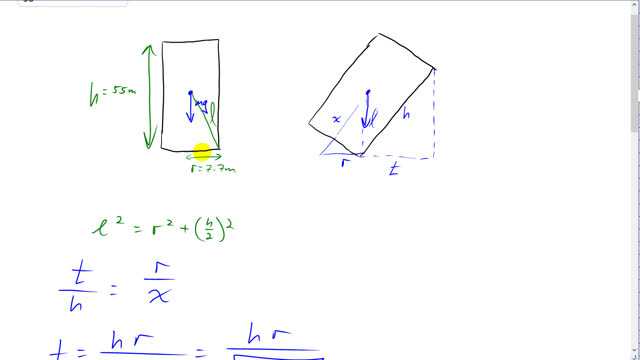
This is Giancoli Answers with Mr. Dychko. Since the tower of Pisa is of uniform construction, the center of mass is in the geometric center of the tower and so long as this center of mass is above the base of support, the tower will be in stable equilibrium. But in this picture here where the center of mass is just above the corner, this is the threshold between being unstable versus stable. Well, actually you would call this an unstable equilibrium technically, it will stay here but just if it's perturbed slightly to the right then there will be a net torque acting to make it fall. So technically, this is unstable equilibrium but this is just the threshold between good and bad. So our job is to figure out what is this distance that the top is from the corner here at this point here where it's about to fall and compare that with how far the top is over currently which is what we are told is about 4.5 meters off center. And this triangle here, this one here, is similar triangle to this one and when I say similar that means that the ratio of corresponding sides are the same and we know they are similar because they have all the same angles inside. So they both have a right angle here and this line is parallel to this line which makes this angle and this angle corresponding angles and so they are equal and well since two angles are the same that means this third angle is the same as well. So all the angles in those two triangles are the same and that means they are similar and that means if we take this side here divided by its hypotenuse then you take the corresponding ratio in the other triangle and those ratio's will be the same. So this side divided by its hypotenuse will be equal. So r divided by x is gonna be the same as t divided by h and our job is to find t. And we can multiply both sides by h and we have t is hr over x whatever this distance is here between the ground and the center of mass. So we know the distance l squared is gonna be r squared—the radius of the base— times the height or the distance to the center of mass which will be the height over 2 squared. So this distance here is h over 2 and this distance x is well, we figure it out by using Pythagoras with l and r. So l squared plus r squared equals x squared and take the square root of that to get x so we are using Pythagoras to figure out x here square root of r squared plus l squared and l squared is r squared plus h over 2 squared as we figured out from this triangle here. And that makes t, the maximum distance that the top can be moved over to the right is gonna be hr over 2r squared plus h squared over 4, all square rooted on the bottom. So that's 55 meters times 7.7 meters on top divided by square root of 2 times 7.7 squared plus 55 meters squared over 4 that gives 14.31 meters is the maximum distance that you can have this top moved over and still have equilibrium. And the tower currently is in stable equilibrium because the top is moved over only 4.5 meters which is less than the 14.3 and if the tower were to lean more 14.31 minus 4.5 meters, if it were to lean 9.8 meters more then it would be an unstable equilibrium and be on the verge of falling.