
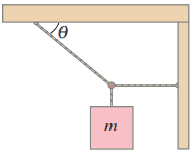
Find the tension in the two cords shown in Fig. 9–52. Neglect the mass of the cords, and assume that the angle is is and the mass is 190 kg.
In order to watch this solution you need to have a subscription.
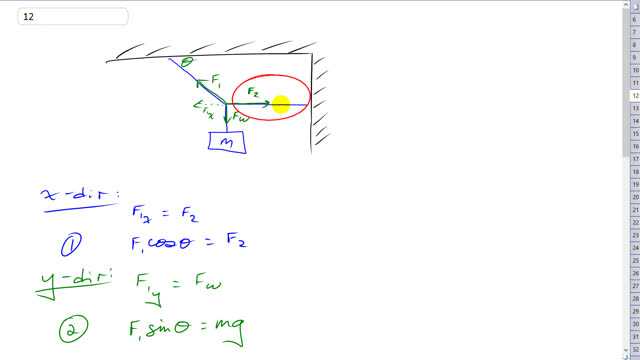
This is Giancoli Answers with Mr. Dychko. The mass that's hanging here exerts a force F w—w for weight—downwards at this point and there's this bit of cord here exerting a tension force F 2 straight to the right and this bit of cord here exerts a force F 1 up on this angle and has an x-component F 1 x straight to the left and then a y-component straight up, F 1 y, and this angle in here is Θ just as the same as this angle because this is parallel to this and these angles are interior opposite angles on opposite sides of the transverse which is here between two parallel lines. So let's consider the x-direction: we'll say that F 1 x force to the left has to equal the force to the right which is F 2 and so F 1 times cos Θ because this is the adjacent leg of this force triangle equals F 2 and then in the y-direction, we say that F 1 upwards y-component has to equal the weight downwards and so that's F 1 times sin Θ—sin because this is the opposite leg— and that equals mg, the weight down. And then there's lots of ways you can combine these two equations to solve for the two unknowns; F 1 and F 2; I have chosen to take equation 2 and divide it by equation 1 so we do each side in turn. So we take the left side, F 1sin Θ, and divide it by the left side of equation 1 which is F 1cos Θ and then take the right side of equation 2, mg, and divide it by the left side of equation 2 which is F 2. And the reason that's useful is because this F 1's cancel and we are left with sin Θ over cos Θ which we have to remember is tan Θ and that's gonna be mg over F 2. And then multiply both sides by F 2 over tan Θ and the F 2 cancels on the right side and appears on the left and then the tan Θ cancels on the left and appears on the bottom of the right and we have F 2 is mg over tan Θ. So that's 190 kilograms times 9.8 newtons per kilogram divided by tan 33 degrees which is about 2900 newtons. And then F 1 is F 2 divided by cos Θ, take this and divide both sides by cos Θ here and F 1 is what we just figured out for F 2—2867.2 newtons— divided by cos 33 which is about 3400 newtons.
Hello. There is a mistake in the snippet answer. F2 should be, indeed, 2900N.
Moreover, I wanted to know why you decided to take equation 2 and divide it by equation 1? If I am not mistaken, you already all have all of the information that you need to find F1 with equation 2, given that theta=33, mass m=190kg. All you would need to find F2 is to plug in F1 into equation 1. Just a thought...
Thank you for your helpful videos!
I agree that it doesn't make sense to do the whole equation division. That ended up confusing me and ended up solving as shown in the book instead.