
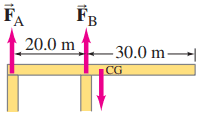
Assume the supports of the uniform cantilever shown in Fig. 9–76 (m = 2900 kg) are made of wood. Calculate the minimum cross-sectional area required of each, assuming a safety factor of 9.0.
In order to watch this solution you need to have a subscription.
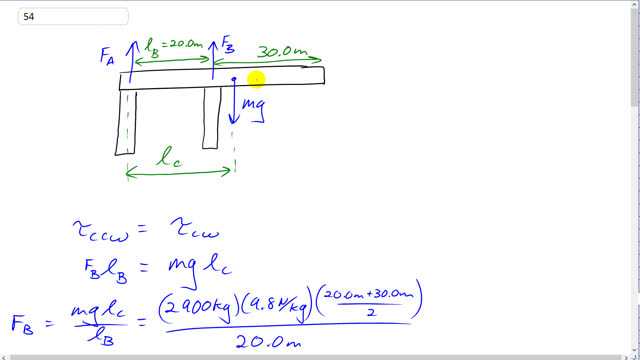
This is Giancoli Answers with Mr. Dychko. So we'll calculate the forces F B upwards and F A upwards exerted on the cantilever and we'll use torque based on knowing also that there's weight acting at the center of this cantilever since it's of uniform mass distribution that torque is clockwise about this pivot which we'll choose to be at the point where force A is acting. So we have the clockwise torque due to the weight equals the counter-clockwise torque due to force B. The lever arm for the clockwise torque due to weight is gonna be the total length divided by 2 and so that's 20.0 plus 30.0 over 2 and multiply by the mass of the cantilever— 2900 kilograms—times 9.8 newtons per kilogram and we divide both sides here by lever arm of support B so we are dividing by 20.0 meters here and that's gonna solve for force B and it's 35525 newtons. So that is the force exerted on the cantilever upwards. And so the force that's on the support is what we are really interested in and that's gonna be the Newton's third-law counterpart to F B. So that's gonna be a force downwards of equal magnitude on the support so this is a compressive force, in other words, F B is being compressed. And that means we use the maximum compressive strength in our formula here for the stress. So the stress on support B is the force exerted on it divided by its cross-sectional area and that's gonna equal the allowable compressive stress and that's gonna be the maximum compressive strength divided by safety factor. So we rearrange this to solve for area; that's gonna be safety factor times F B divided by compressive strength and that's 9.0 times the force exerted on it of magnitude 35525 newtons divided by 35 times 10 to the 6 newtons per square meter. And it gives us two compressive strengths for wood and we want the one that's parallel to the grain because this support is really long and so the wood grain will have to run lengthways. So we get 9.1 times 10 to the minus 3 meters squared has to be the minimum cross-sectional area of that support. Then solving for force A, we know that the total up forces have to equal the total down forces and subtract F B from both sides and you get that the force A is the weight of the cantilever minus F B. So that's 2900 kilograms times 9.8 newtons per kilogram for mg minus 35525 newtons which gives negative 7105 newtons. So F A is actually directed downwards since it's negative and that's the force on the cantilever and we are interested in is the force on the support which is gonna be the Newton's third law counterpart and that's gonna be in the opposite direction of equal magnitude so the force on the support is upwards since it's in the opposite direction to the force on the cantilever. So it's tensile strength is in other words what we need here. So F A divided by the minimum area it's gonna be tensile strength divided by safety factor and so area's gonna be 9.0 times the force 7105 newtons divided by 40 times 10 to the 6 newtons per square meter which gives 0.001599 meters squared and let's call that 1.6 times 10 to the minus 3 square meters never mind the negative sign there because we are just concerned with the magnitudes here.