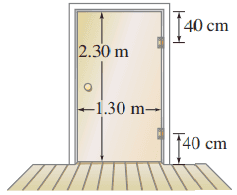
A door 2.30 m high and 1.30 m wide has a mass of 13.0 kg. A hinge 0.40 m from the top and another hinge 0.40 m from the bottom each support half the door’s weight (Fig. 9–69). Assume that the center of gravity is at the geometrical center of the door, and determine the horizontal and vertical force components exerted by each hinge on the door.

VIDEO TRANSCRIPT

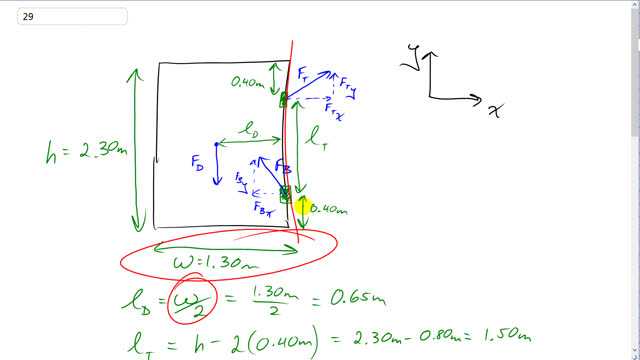
This is Giancoli Answers with Mr. Dychko. The weight of the door is acting in the geometric center of the door so that means it's a distance door width divided by 2 from the right-hand side and that's important because that is the perpendicular distance between the point where the force is acting and our pivot which we'll take to be the bottom hinge. So instead of resolving the force into components, which we could, but instead of doing that, we are taking this position vector you could say between the point where the force is acting and the pivot and finding its perpendicular component and that's l D, lever arm for the door and that's 0.65 meters. And then the other force that's exerting a torque is the horizontal component of the force exerted by the top hinge and that's gonna be a bit to the right there and its lever arm will be its perpendicular distance to the hinge which is just the height of the door minus 2 times 0.4 meters. So minus this gap between the top of the door and the hinge and between the bottom of the door and the hinge. So that's 1.50 meters between F T x and the pivot here at the bottom hinge. So we'll say clockwise torque equals counter-clockwise torque and the clockwise torque is exerted by this F T x x-component of the top hinge multiplied by its lever arm l T and that equals weight of the door times its lever arm l D. And then divide both sides by l T and we get the weight of the door, which I have replaced with mg, times l D divided by l T. So that's 13 kilograms times 9.8 newtons per kilogram times 0.65 meters divided by 1.50 meters and that gives us 55.2 newtons. Now the y-component of the top hinge force and the y-component of the bottom hinge force are equal because the question tells us that each of them bears half the weight of the door so they each are equal to 13 kilograms times 9.8 newtons per kilogram divided by 2 which is 63.7 newtons. And then the only thing we need to find out now is the x-component of the bottom hinge and it has to go to the left with a magnitude equal to the x-component of the top hinge because it means all the horizontal force will have to bounce out but there are only two and so this one has to equal that one and it's going in the opposite direction so we have a negative sign there. So F B x the x-component of the bottom hinge force is the negative of the x-component of the top hinge force so that's negative 55.2 newtons.