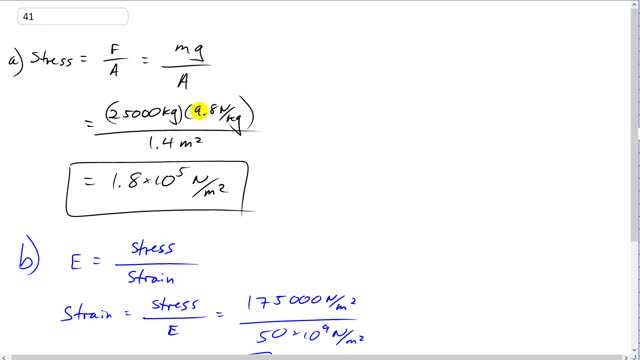
A marble column of cross-sectional area $1.4 \textrm{ m}^2$ supports a mass of 25,000 kg.

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. This stress on the marble column is the force that it's supporting divided by the cross-sectional area of the column. So it's supporting 25000 kilograms which we multiply by 9.8 newtons per kilogram to get the total force applied downwards on the column divided by this cross-sectional area of 1.4 square meters that gives 1.8 times 10 to the 5 newtons per meter squared of stress. Elastic modulus is defined as stress divided by strain and we can rearrange this to solve for strain that is stress divided by the elastic modulus. So that's the answer from part (a)— 175000 newtons per square meter— divided by the elastic modulus for marble which is 50 times 10 to the 9 newtons per square meter and that gives a really small number which we expected— 3.5 times 10 to the minus 6— no units on that because you can also think of strain as being the change in length divided by original length and since we have experience knowing that marble is very uncompressible, you can't squish it, and so we would expect this ratio to be really small; it's change in length as a ratio of its original length should be really small as we see here.