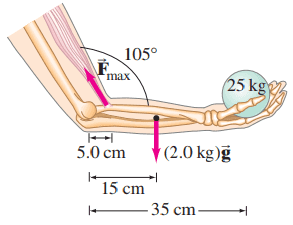
If 25 kg is the maximum mass $m$ that a person can hold in a hand when the arm is positioned with a $105 ^\circ$ angle at the elbow as shown in Fig. 9–74, what is the maximum force $F_{max}$ that the biceps muscle exerts on the forearm? Assume the forearm and hand have a total mass of 2.0 kg with a CG that is 15 cm from the elbow, and that the biceps muscle attaches 5.0 cm from the elbow.

VIDEO TRANSCRIPT

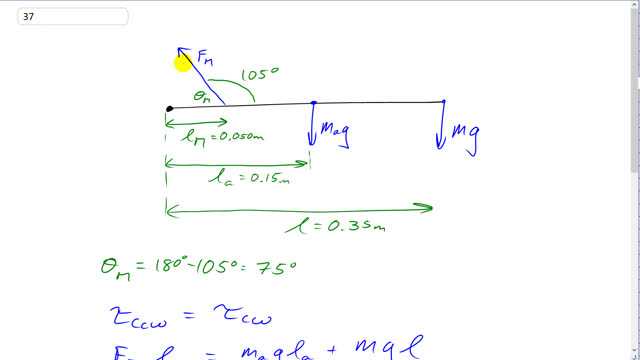
This is Giancoli Answers with Mr. Dychko. The total counter-clockwise torque on the arm has to equal the total clockwise torque. So the bicep muscle is responsible for the counter-clockwise torque and we'll multiply the perpendicular component of this muscle force the component is perpendicular to this position vector linking the place where the muscle is attached to the pivot and that's gonna make the total counter-clockwise torque here and that's gonna be F M times sin Θ M because this is the opposite leg of the triangle here and that's what we'll substitute in here for F M ⊥ F Msin Θ M times l M is the counter-clockwise torque and this Θ M is gonna be 180—the full straight line angle— minus this 105 degrees given to us so that's gonna be 75 degrees. And then for the clockwise torque, it's mass of the arm times g times the distance from the arm center of mass to the elbow joint. So that's lever arm of the arm, 0.15 meters, and then this mass being held in their hand times g times the 0.35 meters— length of the forearm. And so we'll take this and divide both sides by sin Θ Ml M and you get the force exerted by the bicep muscle is gonna be g, which I factored out of these two terms, times mass of the arm times length of the arm plus the mass held in the hand times the entire length of the arm. This is the lever arm of the arm center of mass so you know, it's the 0.15 meters here, not the length of the arm there and that gets divided by sin Θ M times l M. So that's 9.8 newtons per kilogram times 2.0 kilograms times 0.15 meters plus 25 kilograms times 0.35 meters all divided by sin of 75 times the 5 centimeter distance from the muscle attachment point to the elbow which converted to meters is 0.050 meters and that gives 1800 newtons must be the maximum force exerted by the bicep.