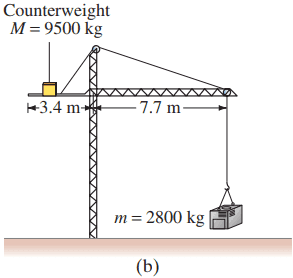
A tower crane (Fig. 9–48a) must always be carefully balanced so that there is no net torque tending to tip it. A particular crane at a building site is about to lift a 2800-kg air-conditioning unit. The crane’s dimensions are shown in Fig. 9–48b.

VIDEO TRANSCRIPT

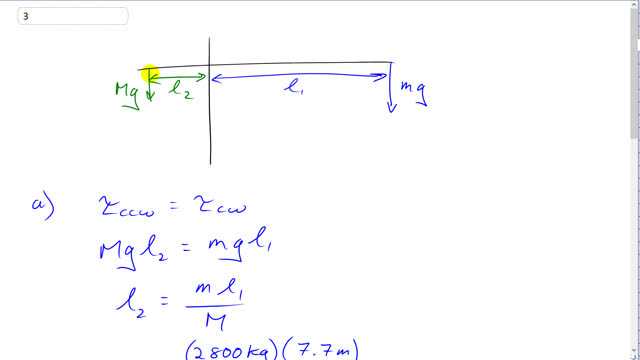
This is Giancoli Answers with Mr. Dychko. A counterweight which is mass M is positioned a distance l 2 from the tower so we'll take the tower to be the pivot point. So l 2 is the lever arm of the weight of this counterweight. And the weight is m times g— acceleration due to gravity or gravitational field strength— and that's the counter-clockwise torque and the counter-clockwise torque has to equal the clockwise torque; the clockwise torque is due to the load that's being lifted which has weight mg and lever arm of l 1. So we'll substitute in for the torque's here: Mgl 2 for the counter-clockwise torque and mgl 1 for the clockwise torque; the g's cancel and divide both sides by M—mass of the counterweight— and you get the position of the counterweight needs to be at, the lever arm that it needs in order to have same torque as the torque due to the load. So l 2 is—the load mass—2800 kilograms times—its lever arm—7.7 meters divided by 9500 kilograms— mass of the counterweight— which gives about 2.3 meters is the distance required from the tower to the counterweight. And then in this part (b), let's assume that the counterweight is extended to its full possible length which according to our drawing is 3.4 meters and assuming that the load is also positioned at the end of the boom, 7.7 meters, what is the maximum mass that the load could have? So the mass m, we'll have to redivide both sides by l 1 is the counterweight mass times the counterweight's maximum lever arm divided by the load's maximum lever arm. So that's 9500 kilograms times 3.4 meters divided by 7.7 meters which is about 4200 kilograms.