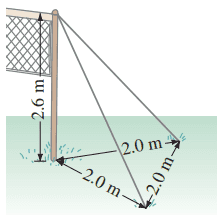
Two wires run from the top of a pole 2.6 m tall that supports a volleyball net. The two wires are anchored to the ground 2.0 m apart, and each is 2.0 m from the pole (Fig. 9–66). The tension in each wire is 115 N. What is the tension in the net, assumed horizontal and attached at the top of the pole?

VIDEO TRANSCRIPT

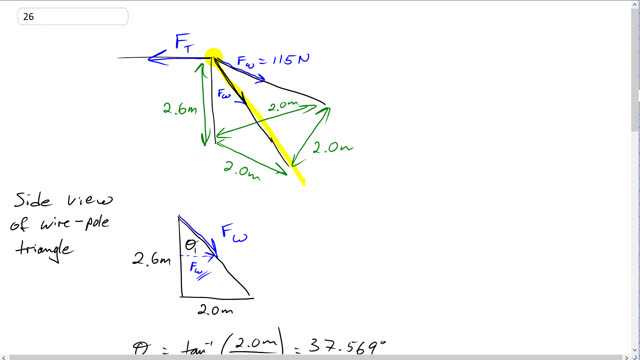
This is Giancoli Answers with Mr. Dychko. We are going to figure out the force of tension on this net here attached to the top of this pole and we are given the tension in each of these guy wires that are anchored to the ground, 115 newtons each, and we are gonna have to figure out the component of this force along the wire which is first of all, parallel to the ground and then find the component of that which is directly opposite to the tension force in the net. So first of all, figure out the force component that's parallel to the ground and we'll look at the side view of the wire-pole triangle so that's this triangle here that's shaded and so we have the wire here 2 meters away from the pole and the pole is 2.6 meters high and the component of the wire force parallel to the ground is gonna be the force in the wire multiplied by sin of Θ 1 this being the opposite leg of this force triangle here and the force triangle is congruent to the wire-pole triangle. So that means Θ 1 is the same angle for each and Θ 1 is the inverse tangent of the opposite over the adjacent so 2.0 over 2.6 and that gives 37.569 degrees and so we'll say that force in the wire of a single wire parallel to the ground is force on the wire times sin Θ 1 force on the wire times sin 37.569 degrees and we'll leave it at that; we could put in the force of the wire 115 but let's jump to the next picture first before we do that. So top-down view of both wires and the pole so now the perspective is with the eyeball up here— looking straight down, give it some blue eyes and some black eyelashes and straight down and there's the pupil. Okay looking straight down here, we see that one wire is a bit to the left and other wire is a bit to the right and these are the components of the wire force that are parallel to the ground and those two have to balance this tension force going straight this way and so we'll have made the axis like this and so we need to find the component of the wire force that's parallel which is in the y-direction. So it's a component of a component you might say; it's the y-component of the parallel component of the wire force. So we have already got the parallel component of the wire force taken care of up here and now to figure out the y-component of it, we multiply by cos of this angle here and that angle is 30 degrees because these forces are directed along the triangle which has side length 2 meters by 2 meters by 2 meters which is an equilateral triangle and equilateral triangle's always have angles of 60 degrees in each corner and this is gonna bisect this 60 degree angle and so it's 60 over 2 which is 30. So we have a parallel component of the wire force times cos 30 gives a y-component of the parallel wire force for one wire and substituted there from our work up here and the tension force in the net is gonna be 2 times that because there are two wires. So that's 2 times force of a single wire times sin 37.569 degrees— this is the component of the wire force parallel to the ground— and then multiply by cos 30 to get the component that is collinear with the net force or in the y-direction here all in the same line as the net force and that gives 2 times 115 times sin 37.569 times cos 30 which gives about a 120 newtons.