
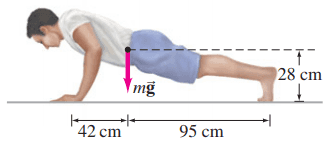
A man doing push-ups pauses in the position shown in Fig. 9–65. His mass m = 68 kg. Determine the normal force exerted by the floor
- on each hand;
- on each foot.
In order to watch this solution you need to have a subscription.
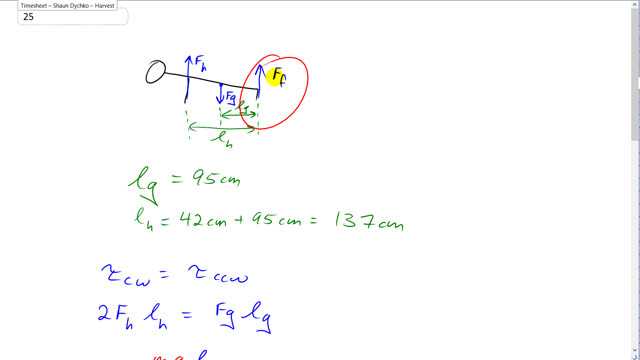
This is Giancoli Answers with Mr. Dychko. The normal force exerted by the floor on the feet and on the hands are both straight up and then there's the force of gravity which is down and we'll take the feet to be the pivot point in which case the force of gravity acting at the center of mass of the person has lever arm l g which is 95 centimeters from their feet we are told in the drawing there and then the hands are exerting a clockwise torque and resulting in a torque equal to F h times the lever arm in the hand which is 42 centimeters from the hand to the center of mass plus the 95 centimeters from the center of mass of the feet for a total 137 centimeters from the feet to the hands. So the clockwise torque has to equal the total counter-clockwise torque and the clockwise torque is the result of the force on both the hands so that's 2 times F h times l h and that equals force of gravity times the gravity's lever arm < i>l g. So divide both sides by 2l h and then substitute mg in place of force gravity there and you have force on each hand is the force on one hand equals mg times l g over 2l h. So that's 68 kilograms times 9.8 newtons per kilogram times 95 centimeters divided by 2 times 137 centimeters and I just left these as centimeters knowing that they would eventually cancel and the only thing that's important is that these distance units are the same; they don't have to be meters although if you did convert them to meters that's fine too. Here 0.95 meters divided by 1.37 meters and that would be the same ratio and you end up with 230 newtons, two significant figures. Then to figure out the force on each foot: you have the total up forces— 2 times the force on a single hand plus 2 times the force on a single foot— equals the total down force which is the gravity mg and we'll subtract 2 times F h from both sides and then divide both sides by 2 afterwards and you get the force on a single foot mg minus 2F h over 2 68 kilograms times 9.8 newtons per kilogram minus 2 times the unrounded answer for the force on a single hand— 231.05 newtons—all divided by 2 which with two significant figures is 1.0 times 10 to the 2 newtons.