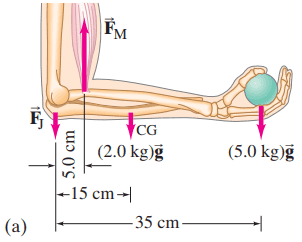
Suppose the point of insertion of the biceps muscle into the lower arm shown in Fig. 9–13a (Example 9–8) is 6.0 cm instead of 5.0 cm; how much mass could the person hold with a muscle exertion of 450 N?

VIDEO TRANSCRIPT

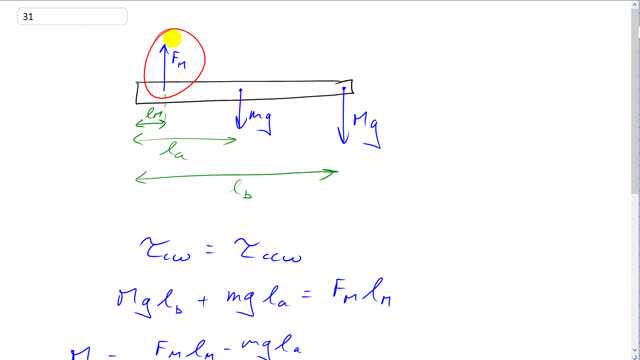
This is Giancoli Answers with Mr. Dychko. With the pivot being at the elbow joint here, there are only three forces that enter into our torque equation. So we have the force due to the bicep muscle upwards here and its insertion point is here, 6 centimeters away from the pivot, and we have the weight of the arm with its center of gravity here at some distance l a for lever arm of the arm and then this ball is in the hand here at the end of the arm with a mass M times g at some distance lever arm b, l b, from the elbow. So the clockwise torque equals the counter-clockwise torque so we have the torque due to the ball mg times l b plus the torque due to the arm, mass of the arm times g times distance from the center of mass of the arm to the elbow equals the force exerted by the muscle times the distance from the muscle to the elbow. And so M, the mass that can be held here, is gonna be, after we take this term to the right hand side by subtracting it from both sides and then dividing both sides by gl b, it's gonna be F Ml M minus mgl a divided by gl b. So we have to look at this picture [9-13a] to figure out all the distances here. So we have 450 newtons is the force applied by the bicep muscle times 6 centimeters converted into meters, 0.060 meters, minus 2 kilogram—mass of the arm— times 9.8 newtons per kilogram times 0.15 meters—distance from the center of gravity of the arm to the elbow joint— all divided by 9.8 newtons per kilogram times 0.35 meters—length of the arm— and that gives about 7.0 kilograms is the maximum ball mass that could be held.