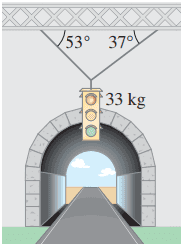
Find the tension in the two wires supporting the traffic light shown in Fig. 9–53.

VIDEO TRANSCRIPT

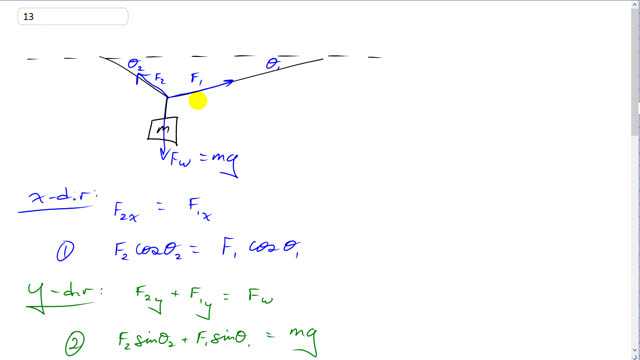
This is Giancoli Answers with Mr. Dychko. This traffic light exerts a force due to its weight mg downwards on this point here where the cables all meet and then this cable to the right here exerts a force F 1 along the length of the cable and F 2 is up along this left hand cable and the components of F 1 and F 2 in the x-direction have to balance out so F 1 x has to equal F 2 x and F 2 x is going this way like that. I guess my drawing isn't quite perfect because this length should be the same as this length but you get the idea anyway. This angle here is Θ 1, the same as this angle because these are both interior opposite angles because these are parallel lines here— this dotted line horizontal there and this horizontal here are parallel— so this angle equals this angle and for the same reason this is Θ 2 in there. So that means F 2 x can be thought of as F 2 multiplied by cos Θ 2—cos because this is the adjacent leg of this force triangle here and then F 1 x is F 1 times cos Θ 1. And then we have to turn our attention to the y-direction because there's nothing we can do with that equation because it has two things that we don't know. So we need a second equation in order to solve for two unknown's. In the y-direction, we have F 2 y component which is going upwards like this F 2 y and add to that F 1 y and those together have to equal the total force downwards which is the weight of the traffic light. So that's F 2 times sin Θ 2— this being the opposite leg of that force triangle for F 2— and plus F 1sin Θ 1 that equals mg and then we have a system of two equations: this one and this one equation 1 and equation 2 and we have to solve for the unknowns F 1 and F 2 because we know everything else here; we know the angles we are given and we are given the mass of the traffic light as well. So let's do it by taking equation 1 and solving for F 2 by dividing both sides by cos Θ 2 and it cancels on the left and ends up with F 1cos Θ 1 over cos Θ 2 on the right and then we'll take that result and substitute it in place of F 2 in equation 2 so equation 2 version b is gonna be F 1cos Θ 1 over cos Θ 2 substituted in place of F 2 and the rest copied unchanged; sin Θ 2 plus F 1sin Θ 1 equals mg. And then this F 1 can be factored out from this term and this term and so we have F 1 times, you know, bracket all this and then divide both sides by that. So we have F 1 equals mg divided by cos Θ 1sin Θ 2 over cos Θ 2 plus sin Θ 1 and then we plug in numbers to solve for F 1. That's 33 kilograms—mass of the traffic light— times 9.8 newtons per kilogram divided by cos of 37 degrees— that's this angle up here and then this angle over here is 53 degrees— so that's times sin 53 divided by cos 53 plus sin 37 and this works out to 190 newtons. And then F 2 we have already figured out is F 1cos Θ 1 over cos Θ 2 so that's 194.63 newtons times cos 37 divided by cos 53 which is about 260 newtons.