
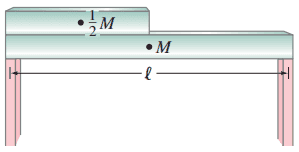
A uniform steel beam has a mass of 940 kg. On it is resting half of an identical beam, as shown in Fig. 9–60. What is the vertical support force at each end?
In order to watch this solution you need to have a subscription.
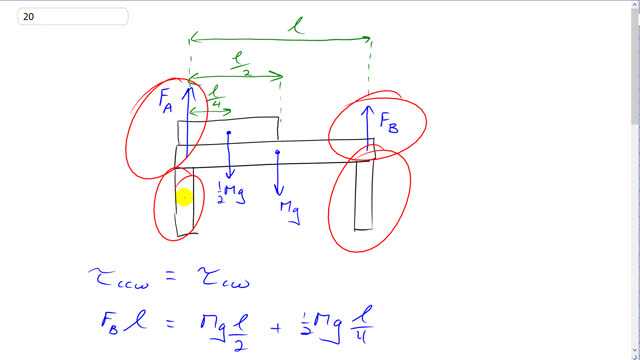
This is Giancoli Answers with Mr. Dychko. There is a force upwards, we'll call it F B due to the support on the right and the force upwards, we'll call it F subscript A for this force by this support going upwards and we have a beam of length l here which is going to be the lever arm for the torque of force B assuming that our pivot is chosen to be here at the position of force A or support A. And that's gonna be the total counter-clockwise torque and then we also have two clockwise torques: one due to the center of mass of this long beam of length l and because it's a uniform beam, the center of mass will be at the geometric center of the beam so it's gonna have a lever arm of the length over 2. And then an identical beam is here of half the length so it's gonna have one-half the mass and its center will be the length divided by 4 or half of, you know, l over 2, whichever way you like to look it. So we have those two clockwise torques: Mg times l over 2 and then plus one-half M times g times its lever arm l over 4 and that total clockwise torque has to equal the total counter-clockwise torque in order for this to be in static equilibrium. So we'll cancel the l on both sides and then we'll just call this Mg over 2 plus Mg over 8 (4 times 2) and then multiply this top and bottom by 4 here to get a common denominator 8 and it's 4 plus 1 so it's 5Mg over 8. And plug that into the calculator, we have 5 times 940 kilograms— mass of the long beam— times 9.8 newtons per kilogram divided by 8 and that gives 5800 newtons when you round it to two significant figures. And then for figuring out force A— the force due to this left hand support— we'll say that all the up forces have to equal all the down forces. So there's two up forces: one due to each support A and B; and then there's two down forces: the weight of the long beam and the weight of the shorter beam. And then subtract F B from both sides to solve for F A and then combine this one-half Mg plus Mg makes 3Mg over 2 multiply top and bottom by 2 if you like and the 2 plus 1 there made 3 and then substitute for F B that we figured out up here, it's 5 times Mg times over 8 so that's what I write here. And so 3Mg over 2 becomes 12Mg over 8 and 12 minus 5 is 7 so we have 7Mg over 8 which is 7 times 940 kilograms times 9.8 newtons per kilogram divided by 8 is 8100 newtons.