
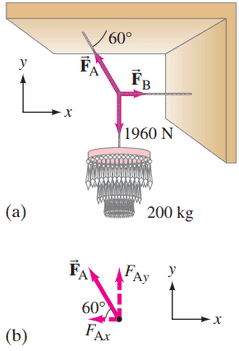
Two cords support a chandelier in the manner shown in Fig. 9–4 except that the upper cord makes an angle of with the ceiling. If the cords can sustain a force of 1660 N without breaking, what is the maximum chandelier weight that can be supported?
In order to watch this solution you need to have a subscription.
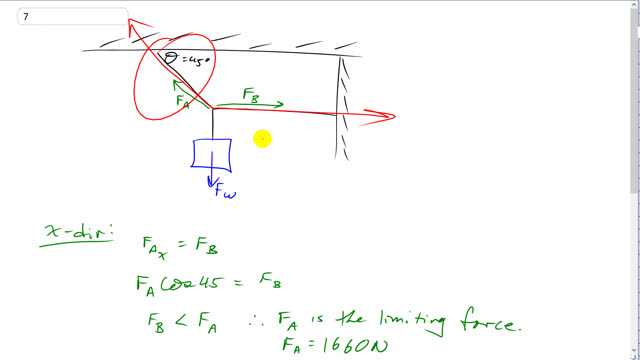
This is Giancoli Answers with Mr. Dychko. This cable here exerts a force A in this direction along this 45 degree angle and force B is directly horizontal to the right and we have this weight of the chandelier straight down. And the x-component F A which is along here has to balance F B so that's why we say here F A in the x-direction equals F B. And F A x is the force A along this hypotenuse multiplied by cos 45 because you know, this being, two parallel lines here this angle in this corner here is the same 45 degrees as this angle because these are interior opposite angles. on opposite sides of the transverse between those two parallel lines. So we'll find F A x by going cos 45 times F A because this is the adjacent leg of that triangle. And based on this here we can see that F B is always gonna be less than F A because cos of anything is always gonna be between 1 and negative 1 so the fancy way of saying that is the range of the cos function is greater than or equal to negative 1 and less than or equal to 1. So either force B is gonna be equal to force A which is really not gonna be the case because it's only a component of force A which has to balance B and the rest of the force A has to go upwards to balance the weight of the chandelier. So this means that F B is always gonna be less than F A since cos of anything is always gonna be less than 1 and if you like, you can calculate cos 45 too if you want to see exactly... it's 0.70 so force B is gonna be 0.7 times force A, it's gonna be 70 percent of force A. Well alrighty! So that means F A is the limiting force and we can make it the maximum, 1660 newtons and then force B will be whatever it is, 1660 times 0.7. And then we turn our attention to the y-direction and say that the y-component of force A has to equal the weight of a chandelier. So that's F A times sin 45 because this y-component is the opposite leg of that force triangle and so that means the maximum weight of the chandelier is the maximum magnitude of force A, 1660 newtons, times sin 45 and that's about 1200 newtons for the maximum weight of the chandelier.