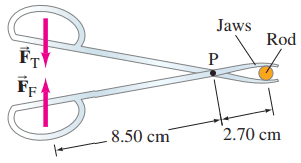
Figure 9–50 shows a pair of forceps used to hold a thin plastic rod firmly. If the thumb and finger each squeeze with a force $F_T = F_F = 11.0 \textrm{ N}$, what force do the forceps jaws exert on the plastic rod?

VIDEO TRANSCRIPT

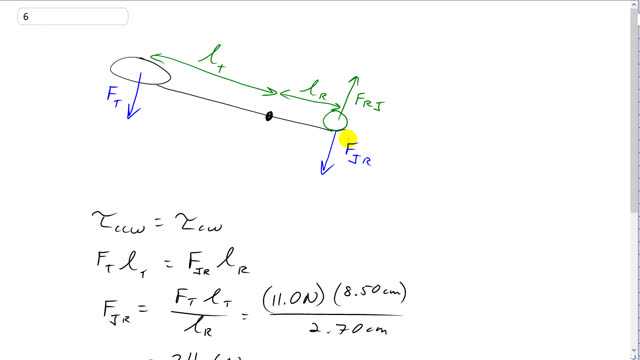
This is Giancoli Answers with Mr. Dychko. Let's consider just one-half of these forceps: here's the top part where your thumb is exerting a force downwards; and here's the pivot there; and then the jaws are here; and this green circle is the rod that is being squished between the jaws of the forceps. And the question is asking us to find the force on the rod due to the jaws and what we are instead gonna think about though is the force on the jaws due to the rod and that's useful because these are Newton's third law pairs and you can tell them because they are in the opposite directions, equal magnitudes and their subscripts are reversed. So Newton's third law pair says that the force on one thing due to another is equal to the opposite— that's what the negative sign means, the opposite direction— of the force on the other thing due to the first and that's the pattern we have here. So we can see that force on the rod due to the jaw, which we have to find, is the opposite or the negative of the force on the jaw due to the rod. So this force here exerts a torque about this pivot and that torque has to be equal to the torque that this force exerts about the same pivot in the opposite direction of course. So this force due to the thumb exerts a counter-clockwise torque equal to the force due to the thumb times the lever arm of the thumb force and that's gonna equal the torque that's clockwise due to the force on the jaws due to the rod times its distance from the pivot and then divide both sides by l T and we get force on the jaws due to the rod is the thumb force—11 newtons—times 8.5 centimeters divided by 2.70 centimeters and we can leave the centimeters as they are— no need to convert them into meters because the units will cancel anyway and the only important thing is that they are the same units— and we have 34.6 newtons. So the magnitude of the force on the jaws due to the rod or it's the same as the magnitude of the force on the rod due to the jaws and anyway, this is what we need to find and so it's gonna be 34.6 newtons.