
A steel cable is to support an elevator whose total (loaded) mass is not to exceed 3100 kg. If the maximum acceleration of the elevator is , calculate the diameter of cable required. Assume a safety factor of 8.0.
In order to watch this solution you need to have a subscription.
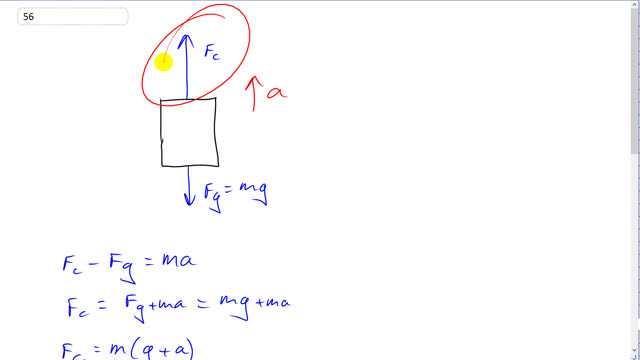
This is Giancoli Answers with Mr. Dychko. We need this free-body diagram of the elevator to figure out what the force exerted by the cable will be. We'll assume that acceleration is upwards— that's the case when this force will be at its maximum; when the elevator is accelerating down at 1.8 meters per second squared, this force in the cable would be smaller so we are considering the case where the force is maximum because that's when it will need to have the greatest diameter and the greatest cross-sectional area in other words so that it can tolerate the maximum stress when it's pulling the hardest. So the force upwards minus the force downwards has to equal mass times acceleration because these two together make the net force and then add F g to both sides and that gives us the cable force is force of gravity in the elevator with all of the occupants inside included plus total mass times acceleration and that's mg plus ma and factor out the m and you get cable force is the mass times acceleration due to gravity plus the acceleration upwards of the elevator. So maximum tensile stress that this cable can tolerate is gonna be force divided by its cross-sectional area which we are gonna solve for at a minimum here and that's gonna equal tensile strength of steel divided by the safety factor and we can rearrange this to solve for A min, take the reciprocal of both sides say, and that puts F on the bottom here and then you can multiply both sides by F and after this is flipped over and you get minimum area is safety factor times the force divided by tensile strength and the area is π times r squared r being half the diameter and so we'll write π times d squared over 4. And then multiply this and this by 4 over π and you get d is the square root of 4 times the safety factor times the force which is m times g plus a that we figured out before with that Newton's second law work with the free body diagram divided by π times the tensile strength and you get square root of 4 times 8—the safety factor—times 3100 kilograms times 9.8 meters per second squared plus 1.8 meters per second squared divided by π times 500 times 10 to the 6 newtons per square meter—tensile strength of steel— and that gives 2.7 centimeters.