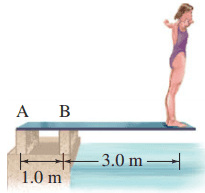
Calculate the forces $F_A$ and $F_B$ that the supports exert on the diving board of Fig. 9–49 when a 52-kg person stands at its tip.

VIDEO TRANSCRIPT

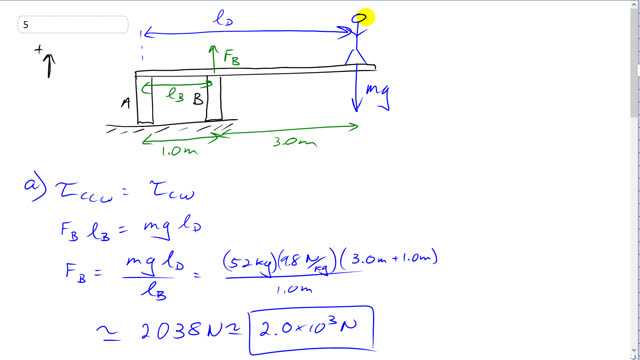
This is Giancoli Answers with Mr. Dychko. Let's consider the first case where the board we assume has no mass so the only forces involved when we are dealing with torque are the force due to the diver— their weight going downwards— and this force due to support B which is exerting a counter-clockwise torque. So there are two torques: the force due to support A exerts no torque because we'll take A to be the pivot point in which case there's no lever arm for force A. So the counter-clockwise torque equals the clockwise torque for anything that is static and that means F B times l B equals mg times l D—mg being the weight of the diver; l D being the diver's lever arm— and force B support force upwards times the lever arm for that force. And divide both sides by l B and we get mgl D over l B is force B. So 52 kilograms times 9.8 newtons per kilogram times 3.0 meters to support B plus an additional 1.0 meter to support A so a total a 4.0 meters between support A and the diver so that's 4 meters here divided by 1 meter lever arm of force B and that gives about 2.0 times 10 to the 3 newtons must be the force B and upwards is the positive direction so this force is upwards. And then to figure out the force that support A exerts, we consider Newton's second law or say that all the up forces have to equal the down forces. So let's assume that force A is upwards in the same direction as force B and so all the up forces are on the left side here and all the down forces are on the right side there's only one that's the force of the diver that's mg downwards so we can solve for F A by subtracting F B from both sides. So we have F A is mg minus F B so that's 52 kilograms times 9.8 newtons per kilogram minus the force that we just figured out for force B and that gives us negative 1.5 times 10 to the 3 newtons and the negative sign means that force A is actually downwards like this that's keeping this m from lifting off so there must be some bolts screwed into the board in order to stick them to the support A. Then in part (b), we say that there is a mass for the diving board and it's gonna be positioned here right in the middle of the diving board that will be m... (do we give it a special name?) m B—yeah mass of the board— times its lever arm which we'll call l B confusingly should have chosen a different letter for that because these are two different lever arms so let's say l BO which is a bit of a bad acronym but anyway we'll go with it: l BO, hopefully that doesn't spell too bad. So we have l B's lever arm of the support B and m Bg times l B overboard— this is the total clockwise torque; the torque due to the board and then the torque due to the diver— and we'll divide both sides by l B and we get that force B in this case now is gonna be higher we expect because now there's additional torque going clockwise so force B will have to have a greater magnitude upwards in order to exert more torque to offset the increase in torque that's clockwise. Force B has to create a counter-clockwise torque equal to this now greater clockwise torque. So we have force B is g times m Bl B plus m Dl D and divided by l B so that's 9.8 newtons per kilogram times 28 kilogram times 2.0 meters lever arm for the board mass plus 52 kilograms—mass of the diver—times their lever arm of 4.0 meters divided by 1 meter lever arm for support force B and that gives about 2600 newtons positive so it's upwards and it's greater than it was before so that meets our expectations there. Always do a bit of a reality check in your answers; if we had an answer here that was less than our answer in part (a), we would be suspicious. Then to figure out the support force A we'll have the same process as Newton's second law saying that the total, you know, sum of the forces equals mass times acceleration and when acceleration is zero that means the total force equals zero but I like to write it as saying up forces total equal the down forces total. So we have F A plus F B equals m board times g plus m diver times g and F A after you subtract F B from both sides and factor out the common factor g if you feel like it. So we have 9.8 newtons per kilogram times 28 kilograms plus 52 kilograms minus 2587.2 newtons and that gives negative 1800 newtons, negative sign meaning it's down.