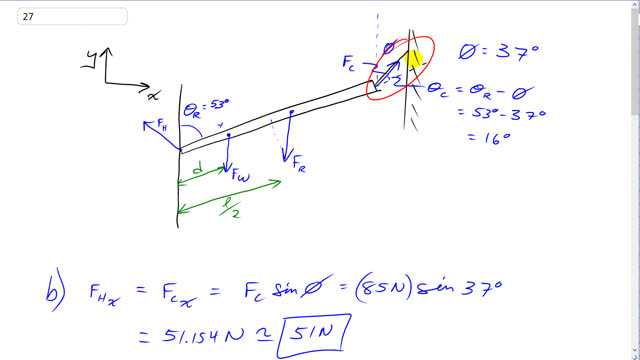
A uniform rod AB of length 5.0 m and mass M = 3.8 kg is hinged at A and held in equilibrium by a light cord, as shown in Fig. 9–67. A load W = 22 N hangs from the rod at a distance $d$ so that the tension in the cord is 85 N.

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. So for part (a), we need a free body diagram which shows all the forces on this rod. So since this is a cord over at this end, the force has to be along the cord because tension forces are always along the flexible string or cord, you can't have any component that's perpendicular because then the cord would bend so that's one force. And then there's the weight of the rod straight down and then there's this hanging weight straight down then there's the force of this hinge which is at some angle because this is, you know, it's not a cord it's a bolt there which can exert forces in both vertical and horizontal directions and I know it's going a little bit to the left because it has to have an x-component that balances the component of the cord force which is in the x-direction and it has to have a y-component which balances both of these forces that are down and so I have got it pointing upwards there although it might actually be down since the cord is also exerting a force upwards so it's hard to tell at this point whether the hinge force is up or down but it certainly is to the left. So the x-component of the hinge force is the same as the x-component of the cord force and that's F csin Φ because if we were to redraw this triangle down here, it would look like this: we have F c at an angle Φ to the vertical... (oops) and we are interested in knowing what this horizontal component of it is. So that's F c x and that's the opposite leg of this force triangle and so we use sin of Φ to get it. So 85 newtons is the cord force we are told times sin 37 gives 51 newtons. And then in the y-direction, the hinge force y-component which is upwards like this, F H y, plus the y-component of the cord force which is this portion here, F c y together have to equal the total down forces which are the weight that's hanging and the weight of the rod, F w plus F R. So we'll subtract F c y from both sides and we have F w plus Mg is the weight of the rod minus F c times cos Φ since it's the adjacent leg of this triangle. And that's 22 newtons plus 3.8 kilograms— mass of the rod— times 9.8 newtons per kilogram minus 85 newtons times cos 37 which gives about negative 9 newtons. So this negative sign means our original assumption that the hinge force is upwards is wrong... well, yeah so it's going in the opposite direction to what we assumed it's going downwards so F H is actually pointing like this. Since the cord has so much vertical component upwards already, the hinge force has to go down to add to the weight of the rod and the weight that's hanging in order to in total compensate for the y-component of the cord force upwards. And then part (c), we have to figure out what this distance is between where the weight's hanging and the hinge and we'll use torque to figure that out. And we know that the clockwise torque has to equal the counter-clockwise torque so clockwise speaking, we have the torque due to the hanging weight and we have the torque due to the weight of the rod and this force is acting at a distance d from the hinge, we'll take the hinge to be the pivot, and we need to multiply d by the component of the weight which is perpendicular to the rod. (Oops) And likewise for the torque due to the weight of the rod, we'll take its component from that force that's perpendicular to the rod multiplied by this distance length of the rod over 2 because this force is acting at the geometric center of the rod since the rod is uniform mass distribution. So the center of mass will be in the physical center of the rod and this component this is F R perpendicular to the rod that component will be F R times sin of Θ R because this wall here and this force here are both straight down and this rod is, you could say, a transverse between them which means that this angle here is 53 degrees equal to Θ R these are interior opposite angles and with this being 53, F R perpendicular is the opposite leg of this triangle here and so we'll use sin Θ or sin 53 times F R to figure out F R perpendicular and this is the same story with the weight as well. So F W perpendicular will also be F W sin Θ R and F R perpendicular is mg times sin Θ R. And multiply by those lever arms, l W and length of the rod over 2 here, and then that equals F C— force of the cord—multiplied by its component well the component of the cord force which is perpendicular to the rod multiplied by the length of the rod. So zooming in on this triangle here now we are looking at just at the bottom portion of it now; if we were to extend the rod here— this black line represents the rod— and the cord is at some angle 37 degrees with respect to the vertical and what we are interested in is knowing this angle in here because then we can go sin multiplied by that to get F C perpendicular. So this is the cord force component which is perpendicular to the rod and then we'll multiply by the length of the rod. So this angle in here is Θ C and it's Θ R because this full angle here is Θ R because this wall and this vertical are parallel lines and this angle here Θ R and this total angle of Φ plus this Θ C in here are corresponding angles and so they are equal. So we have Θ C is Θ R—this whole thing here—minus Φ so 53 minus 37 which is 16 degrees. So we'll take sin of 16 degrees, multiply by F C to get F C perpendicular... okay... and multiply by the length of the rod. So we have to isolate l W— the distance from the hinge to where the weight is hanging— by taking this term to the right hand side so that makes it a minus mgsin Θ R times l over 2 all divided by F Wsin Θ R. So that's 85 newtons times sin 53 minus 37 which is 16 times 5.0 meters (oops, should be an l right there) minus 3.8 kilograms times 9.8 newtons per kilogram times sin 53 times 2.5—5.0 over 2— divided by 22 newtons times sin 53 and that gives 2.4 meters is the distance from the hinge to where this weight is hanging so I guess, well, d is 2.4 meters.