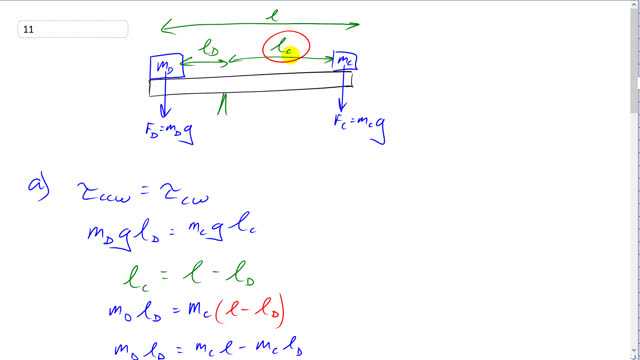
A 75-kg adult sits at one end of a 9.0-m-long board. His 25-kg child sits on the other end.

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. We have the child sitting at one end of the teeter-totter and the dad sitting at the other end and the child has some distance from the pivot— we'll call it the lever arm of the child, l C— and the dad is some distance from the pivot, l D for "dad" and the force down due to the child is the mass of the child times g and for dad, it's mass of the dad times g and these forces and these lever arms together result in some torques about this pivot and the counter-clockwise torque has to equal the clockwise torque. So the counter-clockwise torque is due to the dad and so that's m Dg times the lever arm l D and that equals m Cg times lever arm l C. Now we don't know what l C and l D are let's solve for l D and we'll do that by replacing l C with something containing the letter l D and we can see that l C is gonna be the total length of the beam l take away this distance l D. And so we'll make that replacement here by saying that the lever arm of the child is the total length of the beam minus the lever arm of the dad and then do some algebra to solve for l D. So we'll distribute the m C into the brackets there and make it m C times l minus m C times l D, bring this term to the left hand side which makes it positive and factor out the common factor l D and we could l D times m D plus m C equals m Cl and then divide both sides by this bracket m D plus m C. And that ends up being m C times l over the total masses and so that's mass of the child—25 kilograms— times 9 meters divided by 75 kilograms plus 25 kilograms which makes the lever arm for the dad 2.3 meters that's where the pivot should be placed 2.3 meters from the dad. In part (b), we add the complication that this beam now has some mass and so since it's a uniform beam that means we can consider the weight of the beam to be acting in its center and that's the force of the beam and its the mass of the beam times g and it has some lever arm let's call this l B for lever arm of the beam and that l B is gonna be half the beam length minus lever arm of the dad. So that's l over 2 minus l D that's what I have written for l B and this lever arm of the child, I just put in l minus l D which we figured out before. And rewriting this now, substituting for l B, lever arm of the beam, we get this whole thing and then we have to distribute the masses into the brackets there, multiply through and then collect all the terms containing lever arm of the dad on the same side of the equation. So we multiply through here and ended up with all these terms and then this term here goes to the left side by adding it to both sides and then add this to both sides and you end up with three terms on the left all containing l D which we can factor out and so it's l D times m D plus m B plus m C equals these two terms which will remain on the right hand side and have a common factor l which we factor out and so it becomes l times m B over 2 plus m C. And so l D, after you divide both sides by this bracket, is l times m B over 2 plus m C over the total mass. So that's 9 meters times 15 kilograms— mass of the beam—over 2 plus 25 kilograms—mass of the child— divided by 75 kilograms plus 15 plus 25 and that gives 2.5 meters from the dad is where the pivot should be placed when you consider the beam having a mass.