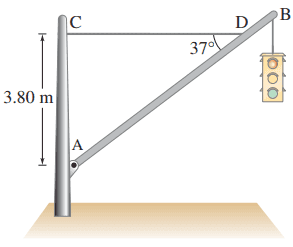
A traffic light hangs from a pole as shown in Fig. 9–59. The uniform aluminum pole AB is 7.20 m long and has a mass of 12.0 kg. The mass of the traffic light is 21.5 kg. Determine

VIDEO TRANSCRIPT

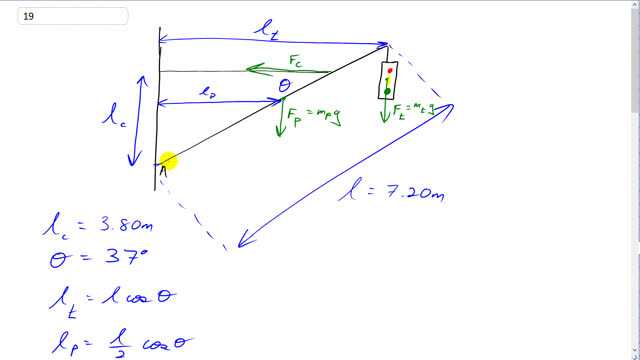
This is Giancoli Answers with Mr. Dychko. So in blue on this picture I have shown all the distances lever arm's and so on and in green, I'm showing all the forces. Well, I guess I forgot to put the hinge force on here... here's the hinge force is going somewhat to the right and somewhat upwards. So we are gonna figure out the cable force first in part (a) and when we are dealing with torque, we have to multiply a force by a distance to the pivot and these two things have to be perpendicular. So either we resolve the force into components that are perpendicular component of the force multiplied by the distance between the point where the force is applied to the pivot or we take the force as is— which is the method I'm gonna use— we take the force as is like the force on the pole for example, straight down, due to its weight multiplied by the perpendicular component of the distance to the pivot. So this is the lever arm for the weight of the pole because the force on the pole is straight down due to gravity and to get to the pivot which is along this line here, along the pole, to get to that pivot perpendicularly, we'd have to go like this all the way to this point here and this point here is directly above the pivot. And so it's this component of, you know, the position vector you might say there's this position vector between the point where this force is applied and the pivot going like that and it's this component which is perpendicular that we need in order to calculate torque and so it's this component that we'll multiply by the force to get the torque due to the weight of the pole. And it's the same story with the traffic light so we'll take the force going straight down say and then multiply it by the perpendicular component of the position vector between the traffic lights and the pivot so that's along this line here l t—lever arm for the traffic light. So that's the approach I have used here. You could instead take the entire length of the pole as the lever arm for the traffic light and then find the component of the force of the traffic light that is perpendicular to that, that would be fine too. Okay. So let's proceed here: we have lever arm for the cable force is given to us in this 3.80 meters and that's the perpendicular distance to the pivot between the line of action of the cable force here and and the pivot and then the angle here Θ is 37 degrees and that's the same Θ as in here, as in here because all these lines are parallel and and this is a transverse going through all those parallel lines and so these angles are all corresponding angles; corresponding angles are equal. So lever arm for the traffic light is gonna be the full length of the aluminum pole that's holding it up multiplied by cos Θ because this is the adjacent leg of the position vector between the traffic light and the point A, the hinge. And for the pole, the center of mass of the pole is gonna be in the middle of the pole so at a position of l over 2 from the pivot at A and to find its component perpendicular to the weight, we go l over 2 times cos Θ. And so now we talk about torques. So the torque counter-clockwise is due to the cable and it's the cable force then multiplied by the cable's lever arm and that equals the force due to the pole times the pole's lever arm plus the force due to the traffic light— the weight of the traffic light— times its lever arm l t. And then divide both sides by l C and then substitute for each of these forces on the pole and on the traffic light. So we have the weight of the pole is the mass of the pole times g times its lever arm l over 2 times cos Θ plus the mass of the traffic light times g times its lever arm of l times cos Θ and all that's divided by l C. And you can factor out those common factors: g, l and cos Θ from both these terms and top and you have glcos Θ times mass of the pole over 2 plus mass of the traffic light all divided by lever arm of the cable. So that's 9.8 newtons per kilogram times 7.20 meters—length of the pole— times cos 37 times 6 kilograms, 12 over 2, plus 21.5 kilograms—mass of the traffic light— all that's divided by 3.80 meters and that gives about 410 newtons of tension in the cable. So when we are talking about the hinge, the x-component of the hinge force has to equal the cable force the cable force is entirely in the x-direction to the left and so the hinge has to exert a compensating force of equal magnitude to the right and so that's just gonna be 410. And then the y-direction, the hinge as to exert a force upwards to compensate for the total of the weight of the pole down and the traffic light down. So total up forces have to equal total down forces and so hinge y-component upwards is equal to the pole weight down plus the traffic weight down. And so that's m P times g plus m t times g, factor out the g and we get 9.8 times 12 kilograms plus 21.5 kilograms and this makes 328 newtons must be the y-component of the force exerted by the hinge.