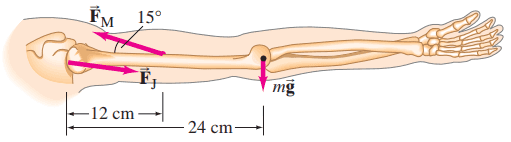
Suppose the hand in Problem 34 holds an 8.5-kg mass. What force, $F_M$, is required of the deltoid muscle, assuming the mass is 52 cm from the shoulder joint?

VIDEO TRANSCRIPT

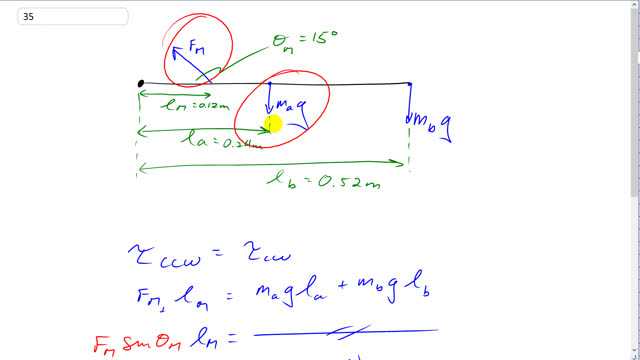
This is Giancoli Answers with Mr. Dychko. This deltoid muscle force is exerting a counter-clockwise torque to balance the two clockwise torques which are exerted by the mass of the arm and the weight of the ball. So the weight of the arm is mass of the arm times g and the weight of the ball is mass of the ball times g and the arm has a lever arm of 0.24 meters from the shoulder joint pivot and the ball has a lever arm l b of 0.52 meters from the shoulder joint. And so counter-clockwise torque equals clockwise torque F M ⊥ times l M is the counter-clockwise torque so that's the perpendicular component of the muscle force so the part that's perpendicular to this position vector linking the point where the force is acting or the muscle's attached to the shoulder joint. And that perpendicular component is F M times sin of Θ M; it's sin because it's the opposite leg of this force triangle. So we have F Msin Θ M times l M— lever arm of the muscle— equals the total clockwise torque and divide both sides by the sin Θ Ml M and you are left with F M on the left side equals g factored out from both those terms times M al a plus M bl b divided by sin Θ Ml M. So that's 9.8 newtons per kilogram times 3.3 kilograms—mass of the arm— times 0.24 meters— distance from the center of mass of the arm to the shoulder joint— plus 8.5 kilograms—the mass being held in the hand— times its distance of 0.52 meters from the shoulder joint all divided by sin 15 times 0.12 meters— distance from the muscle to the shoulder joint— and this gives 1600 newtons is the force exerted by the deltoid.