
Three children are trying to balance on a seesaw, which includes a fulcrum rock acting as a pivot at the center, and a very light board 3.2 m long (Fig. 9–57). Two playmates are already on either end. Boy A has a mass of 45 kg, and boy B a mass of 35 kg. Where should girl C, whose mass is 25 kg, place herself so as to balance the seesaw?
In order to watch this solution you need to have a subscription.
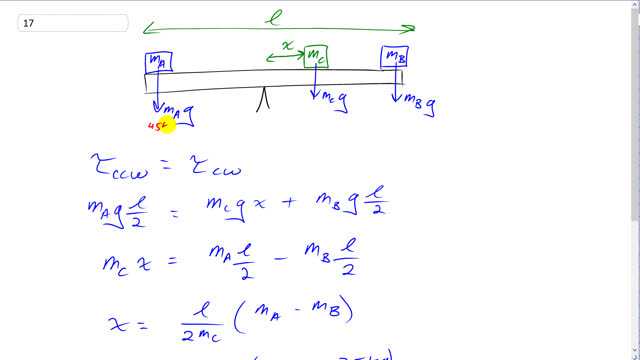
This is Giancoli Answers with Mr. Dychko. There's boy A positioned at the left end of the teeter-totter and boy B positioned here at the right end of the teeter-totter; boy A has mass of 45 kilograms and boy B has a mass of 35 kilograms and this fulcrum or the pivot is in the middle of the teeter-totter. So that means this is not going to be balanced when there's just boy A and boy B because they have a same lever arm, l over 2, from the pivot but they have different masses so their torques will not be equal. And there needs to be more clockwise torque and so that's what this girl is gonna provide by positioning herself here some distance x from the pivot such that her torque plus the torque of mass B is gonna equal the torque due to boy A. So the counter-clockwise torque has to equal the clockwise torque in order to have equilibrium; counter-clockwise torque is due to mass A times g—that's the total weight downwards— times the lever arm l over 2 and that equals the weight of the girl m C times g times her lever arm x plus m Bg times the lever arm of boy B, l over 2. And the g's cancel and so we have m Cx equals, after we take this to the left hand side by subtracting it from both sides, m A times l over 2 minus m B times l over 2 where I have also switched the sides around so that I have the term containing the 'x' on the left side. And then factor out the l over 2 which is a common factor here so you get l over 2 times m A minus m B and also divide both sides by m C or multiply by 1 over m C—however you like to look at it— and you end up with l over 2m C times m A minus m B. So that's 3.2 meters divided by 2 times 25 kilograms times 45 minus 35 kilograms which gives 0.64 meters is the distance the girl has to position herself from the pivot on the side of the lighter boy.