
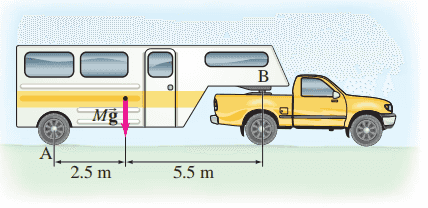
A 2500-kg trailer is attached to a stationary truck at point B, Fig. 9–61. Determine the normal force exerted by the road on the rear tires at A, and the vertical force exerted on the trailer by the support B.
In order to watch this solution you need to have a subscription.
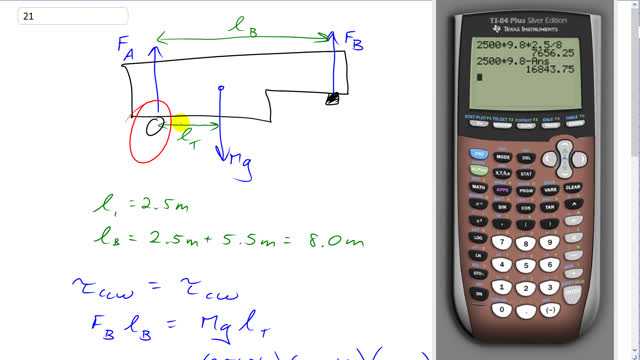
This is Giancoli Answers with Mr. Dychko. We'll choose our pivot to be at the wheel here where there's the normal force F A acting upwards and it's gonna have no torque if we choose the pivot to be there. So then we are dealing with torque, there's only gonne be two of them: one due to this force B due to the support on the truck going upwards; and another torque clockwise due to the weight of the trailer acting down. And the weight of the trailer has a lever arm l T we'll say equal to 2.5 meters and F B will have a lever arm of 2.5 plus 5.5— according to our drawing there— which is a total of 8.0 meters away from the wheel. So the counter-clockwise torque due to F B gets multiplied by l B that equals the clockwise torque, weight of the trailer times the trailer's lever arm. And we'll divide both sides by l B to solve for F B and we have 2500 kilograms— mass of the trailer— times 9.8 newtons per kilogram times 2.5 meters—lever arm for the trailer's weight— divided by 8.0 meters—lever arm of the F B, distance from the wheel— and that gives 7.7 times 10 to the 3 newtons when you round it to two significant figures. And then to figure out F A, we know that the total up forces have to equal all the down forces and so we have F A plus F B, both upwards, and we'll subtract F B from both sides and we get F A is the weight of the trailer minus F B. So that's 2500 kilograms times 9.8 newtons per kilogram minus the unrounded answer for F B and because we don't want intermediate rounding error so we plug in 7656.25 newtons and this gives 1.7 times 10 to the 4 newtons.