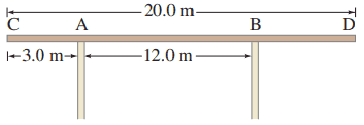
A 20.0-m-long uniform beam weighing 650 N rests on walls A and B, as shown in Fig. 9–62.

VIDEO TRANSCRIPT

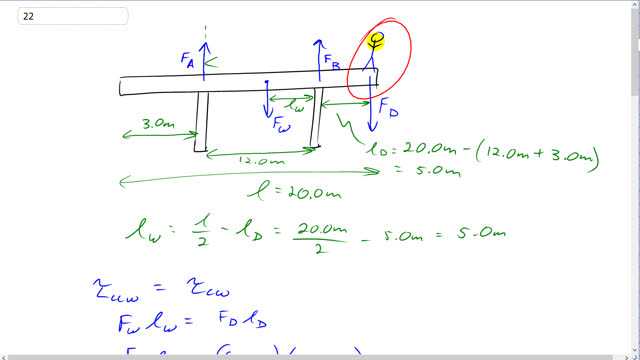
This is Giancoli Answers with Mr. Dychko. When this person is standing at this point D at the very end of this table and they are at the maximum weight possible that will be just the point where there's no force A this beam will be just barely starting to lift off of support A and pivoting about the support B and so force A will be zero for this initial question in part (a). So we'll take support B to be the pivot and there will be two torques: one that's going clockwise due to the weight of this person, F D, and the other one going counter-clockwise due to the weight of the beam here we'll call it F W for weight. And F W will have a lever arm l W— that's the distance from support B— and the person will have a lever arm l D for the lever arm to this point D. Okay. So lever arm D is gonna be the full length of the beam of 20 meters minus the 12 meter separation between A and B and also this 3 meter overhang from A to the left end. So that's gonna be total of 5 meters from point D to the support B. And then lever arm for the weight of the beam will be its position in the middle of the beam, l over 2, minus this amount of overhang here. So it will be l over 2 from the end to the middle of the beam minus the overhang Fl D and that gives 20 over 2 minus 5 which will make 5.0 meters. So the torque counter-clockwise the weight times l W and that equals the torque clockwise which would be the weight of the person F D times l D and we'll figure out this person's weight now; it's gonna be 650 newtons times 5.0 meters— l D—divided by... or sorry l W but anyway, they are both 5.0 meters so l W divided by l D which is also 5.0 meters so 5 over 5 is 1 so F D is 650 newtons. So the maximum weight of the person is 650. Now in part (b), we say what are the forces exerted by the support's A and B when this person is at this position D? Well, we just said that force A is gonna be zero because this person is at their maximum weight such that the beam is just starting to pivot and rotate about this point B and so F A is zero. And then the total up forces have to equal the total down forces so F A plus F B equals F W plus F D and I'm just being thorough here by writing this F A business around— I mean we know it's zero so it doesn't even matter but let's just do it anyway. So we have F W plus F D minus F A is 650 newtons—the weight of the beam— plus 650 newtons—weight of the person— minus 0 for F A gives 1300 newtons for the force exerted upwards by support B. And both of these numbers are precise to the tens place and so our answer is also precise to the tens place this is, you know, '0.000' so that's, you know, got lots of precision and it's precise to the ones place if you just look at it as having one significant figure. Either way, these numbers are the limiting precision on our answer here they are precise only to the tens place and so our answer is precise to the tens place and we'll write it as 1.30 times 10 to the 3 newtons. And then for part (c), suppose this person is now moved so that they are 2 meters away from support A so they are positioned here and so F D is moved over there as well. And now we need to know the distance from support B—we still are considering this to be our pivot point— and their distance is this which we'll label l D prime and that's gonna be this 12 meters between A and B minus the 2 meters that's here between A and the person. So l D is now 12.0 meters minus the 2.0 meters from the person to the support A and so that's 10.0 meters. And we have two counter-clockwise torques now: one due to this person's weight and one due to the beam and then there's one clockwise torque due to force A. And the clockwise torque is gonna be force A times lever arm A— the distance from A to B which is 12 meters— and then we have force D times the new lever arm l D prime plus the weight of the beam times its lever arm l W which is the same as before and divide both sides by l A and switch the sides around and you get F A is gonna be 650 newtons—force due to the person, their weight— times l D prime, 12 minus 2 which is 10, plus 650 newtons times 5.0 meters— distance between the center of mass of the beam and support B— and divide by 12 meters—lever arm of force A— and that's 810 newtons for the force due to support A. And then the support B well, force A plus force B are both upwards and so the total upwards forces has to equal the total downwards forces and we'll subtract F A from both sides and we have F B is weight of the person plus the weight of the beam minus the force upward due to the support A. So that's 650 newtons plus 650 newtons minus 812.5 newtons and that's about 490 newtons for F B in this case.