
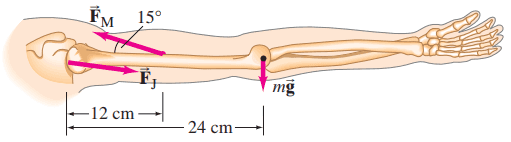
- Calculate the magnitude of the force, , required of the “deltoid” muscle to hold up the outstretched arm shown in Fig. 9–72. The total mass of the arm is 3.3 kg.
- Calculate the magnitude of the force exerted by the shoulder joint on the upper arm and the angle (to the horizontal) at which it acts.
In order to watch this solution you need to have a subscription.
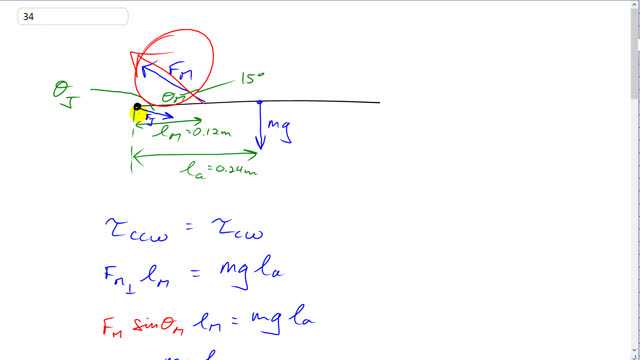
This is Giancoli Answers with Mr. Dychko. The deltoid muscle exerts a force at an angle of 15 degrees in this direction and it's attached 12 centimeters away from the shoulder joint which will be the pivot and the shoulder joint also exerts a force but it will have no torque since we are choosing the pivot to be at the position where the shoulder joint force is acting. And then the center of mass of the arm is here has a weight of mg and it's a distance 0.24 meters from the shoulder joint and so to find F M, we will consider torques and and we'll say that counter-clockwise torques have to equal the clockwise torques. And the counter-clockwise torque is due to the component of F M which is perpendicular to the arm that's F M ⊥ that multiplied by the lever arm for the muscle, 0.12 meters, and that's gonna equal the clockwise torque which is mg times lever arm of the arm. And the perpendicular component of F M is F M times the sin of Θ M because this is the opposite leg of this triangle here and then divide both sides by sin Θ M times l M and you get the force of the muscle is mg—lever arm of the arm— divided by sin Θ M times l M. So that's 3.3 kilograms—mass of the arm— times 9.8 newtons per kilogram times 0.24 meters—lever arm of the arm— divided by sin 15 times 0.12 meters which is about 250 newtons. And then for the force of the joint in the x-direction, it's gonna equal the force of the muscle in the x-direction because those are the only two forces that are going horizontally and so they have to balance each other and the force of the muscle in the x-direction is F M times cos Θ M because that's the adjacent leg of this muscle force triangle. So that's 249.9 newtons times cos 15 which is 241.39 newtons and then the y-component of the shoulder joint force is going downwards this is F J y and that's added to the weight of the arm, mg, downwards and those two in total have to equal the y-component of the muscle which is F M ⊥ on this picture as well. So the y-component of the shoulder joint force is gonna be the y-component of the muscle force minus mg when you take this to the right hand side. So that's F M times sin Θ M minus mg: 249.9 times sin 15 minus 3.3 kilograms times 9.8 newtons per kilogram which is 32.339 newtons. And then to get the resultant magnitude of the shoulder joint force, we'll take the square root of the sum of the squares of the components for the shoulder joint—and this is Pythagoras— and so we have square root of 241.389 newtons squared plus 32.339 newtons squared which is about 240 newtons. And then the angle of that force is gonna be the inverse tangent of the y-component divided by the x-component. So that's inverse tangent of 32.339 newtons divided by 241.389 newtons and this gives us a final answer for the shoulder joint force of 240 newtons at an angle of 7.6 degrees below the horizontal.