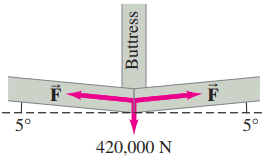
The subterranean tension ring that exerts the balancing horizontal force on the abutments for the dome in Fig. 9–34 is 36-sided, so each segment makes a $10 ^\circ$ angle with the adjacent one (Fig. 9–77). Calculate the tension F that must exist in each segment so that the required force of $4.2 \times 10^5 \textrm{ N}$ can be exerted at each corner (Example 9–13).

VIDEO TRANSCRIPT

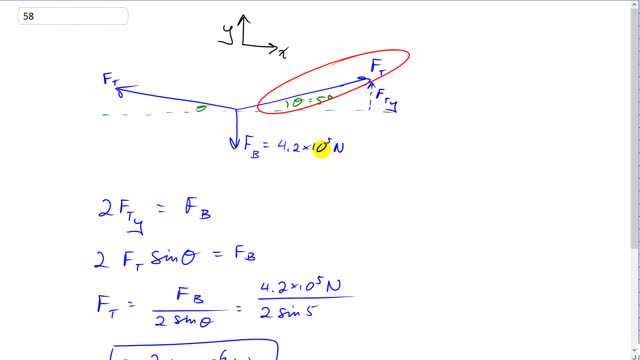
This is Giancoli Answers with Mr. Dychko. The tension force in this tension ring has to balance this force exerted by the buttress on the tension ring. So the buttress force is 4.2 times 10 to the 5 newtons straight down and the y-component of the tension force will balance that and there's gonna be two of them, two y-component's of the tension forces because there's two segments to this tension ring here. So we have two times the y-component of the tension force on one of them in total equals the buttress force and the y-component is gonna be the opposite leg of this triangle here and so we use sin of Θ times F T to calculate it. So F Tsin Θ times 2 equals the buttress force and then divide both sides by 2sin Θ and you get the buttress force 4.2 times 10 to the 5 newtons is divided by 2 times sin of 5 which gives 2.4 times 10 to the 6 newtons is the tension force in each segment of the tension ring.