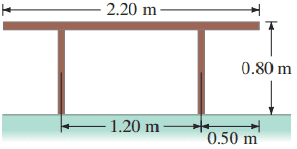
How close to the edge of the 24.0-kg table shown in Fig. 9–54 can a 66.0-kg person sit without tipping it over?

VIDEO TRANSCRIPT

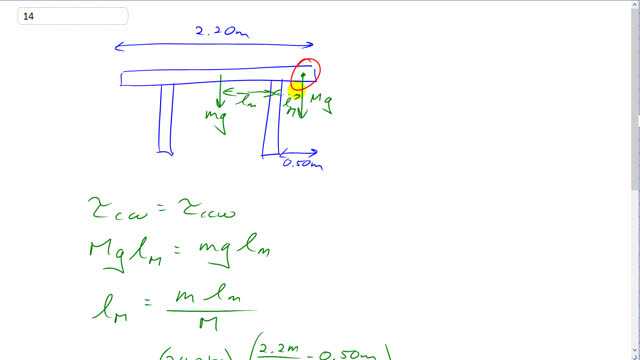
This is Giancoli Answers with Mr. Dychko. So there's a person that's gonna be sitting here somewhere close to the edge of the table some distance l subscript M from the support here, this leg of the table. This l M is gonna be the lever arm for the torque exerted by this person sitting there and at this limit or this point where they just begin to tip the table, the support will basically not be resting on the ground at all so it's just at that threshold where there's no force on it so it exerts no torque. And we have the torque due to the person going clockwise about this pivot here equaling the torque going counter-clockwise due to the mass of the table. So we have M—mass of the person— times g, that's their weight times their level arm l M equals mass of the table times g times the table's lever arm the distance from the center of gravity of the table which is going to be the center of the table since it's of uniform mass distribution and that distance from there to this table leg. And we'll divide both sides by M—mass of the person—and cancel the g's as well and we get the lever arm for this person l M equals mass of the table times the table's lever arm divided by the mass of the person. Now the table lever arm, we calculate by taking the full length of the table, 2.20 meters, divide that by 2 and that gives us the distance from the edge of the table to the center and then subtract away this 0.50 to get this distance from the leg to the center of the table. So that's what's happening here— 2.20 over 2 minus 0.50— and divide by 66 kilograms times by 24 and you get 0.2182 which does not answer our question. This is the lever arm of the person— the distance from the table leg— and the question's asking us for the distance from the person to the edge of the table. So we take this 0.50 meters between the edge and the leg and subtract away the distance from the person to the leg so that's 0.50 minus this answer that we just found and that gives us 0.28 meters is the minimum distance where the closest the person can get to the edge of the table before it tips over.