
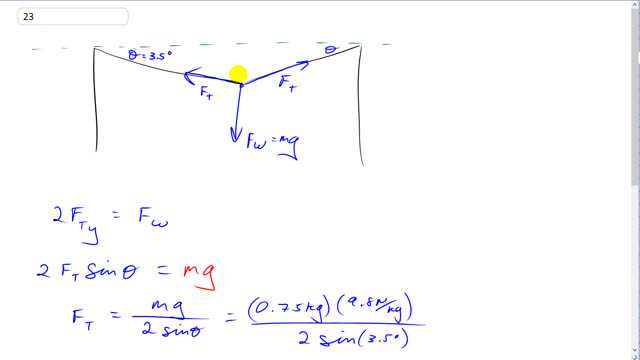
A 0.75-kg sheet is centered on a clothesline as shown in Fig. 9–63. The clothesline on either side of the hanging sheet makes an angle of with the horizontal. Calculate the tension in the clothesline (ignore its mass) on either side of the sheet. Why is the tension so much greater than the weight of the sheet?

In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. The tension in this clothes line goes from this point where the sheet is hanging to the right and upwards and also upwards into the left. And it's the vertical component of the tension which is supporting the sheet so this is F tension y-component but there's a y-component from the tension on both sides of the sheet so we multiply that by 2. And so we have the horizontal component of the tension going to the right and then horizontal component of the tension also going to the left and those balance out to make zero force to the left and right (net force). And then upwards we have the 2 times the tension force has to equal and balance the weight of the sheet going downwards. So this angle here, 3.5 degrees, between the horizontal and the clothes line is equal to this angle in here. So here's our force triangle: horizontal, vertical and hypotenuse and the right angle is here and that makes this vertical component of the tension the opposite leg of this triangle and so we use sin multiplied by Θ times the tension force to get this vertical y-component. So we have 2 times F T sin Θ is the weight of the sheet mg and divide both sides by 2sin Θ and you solve for the tension is mg over 2sin Θ. So that's 0.75 kilograms times 9.8 newtons per kilogram divided by 2 times sin 3.5 and gives about 60 newtons which we'll write as 6.0 times 10 to the 1 in order to show that it has two significant figures. And the tension force is much greater than the weight of the sheet— the weight of the sheet is only about 7 newtons, 0.75 kilograms times 9.8— and this is because only the vertical components of the tension force are supporting the weight so it's not the tension force that's supporting the weight, it's the vertical component of the tension force which is supporting the weight and because this angle is small, the tension force needs to be compensatingly larger in order to have this vertical component be big enough to support the weight. And if you wanna think of it algebraically, sin Θ is small and Θ is small because the graph of sin Θ looks like this where here is 0 and here's 180 and here's 90. So when Θ is small, sin Θ is really small as well and so when we divide by a small number, the quotient or the answer to the division will be large and so when Θ is small, this fraction is gonna be large and so the tension is large when Θ is small.